问题提出

工业生产过程中会产生大量的数据，比如电压、温度、流量等等，不同的工况条件下，数据的走势不同，比如产量稳定时，流量走势平稳，产量增加时，流量势必也会增加，体现在图像上就是流量曲线上升。

比如下图：

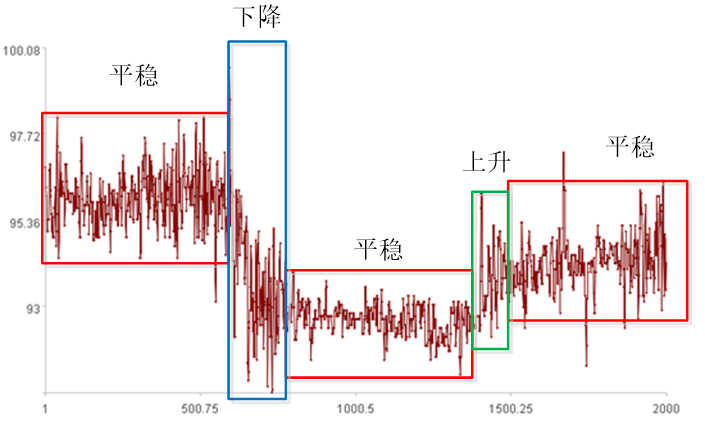
上图中的曲线总体看起来有个趋势，但从细节来看，抖动非常剧烈，如何从剧烈抖动的数据中找出总体趋势呢？这是我们要解决的第一个问题。

如果我们可以得到曲线的总体趋势，把曲线不同趋势看作不同工况，上图大致分为5段工况，分别是平稳——下降——平稳——上升——平稳。

当然，工况是一种通俗的表述，曲线的各种形状都可能是一种工况，我们希望找到具有某种特征的工况区间，比如平稳、振荡发散等。但是什么叫平稳，什么叫做振荡发散呢，还有很多其他工况，我们又该如何识别和定义呢？这是我们要解决的第二个问题。

算法思路

先来思考问题一：如何描述数据的整体趋势？

我们可以参考股票的K线图，它除了每日的K线外，通常还有5日均线、10日均线等，炒股时通常参考这些均线来查看股价的走势。我们也可以考虑用同样的方法算出工业数据的趋势线，用不同的移动窗口得到不同级别（如分钟级、小时级、天级等）的趋势线。

趋势线的方法不止有均线这一种，还有很多其他方法能够得到更适合工业数据的趋势线，由于方法比较多且计算过程比较复杂，这里就不过多介绍了，和移动均线要描述的内容是一样的，不影响理解总体算法思路。

下图是用一种加权拟合方式算出的趋势线：

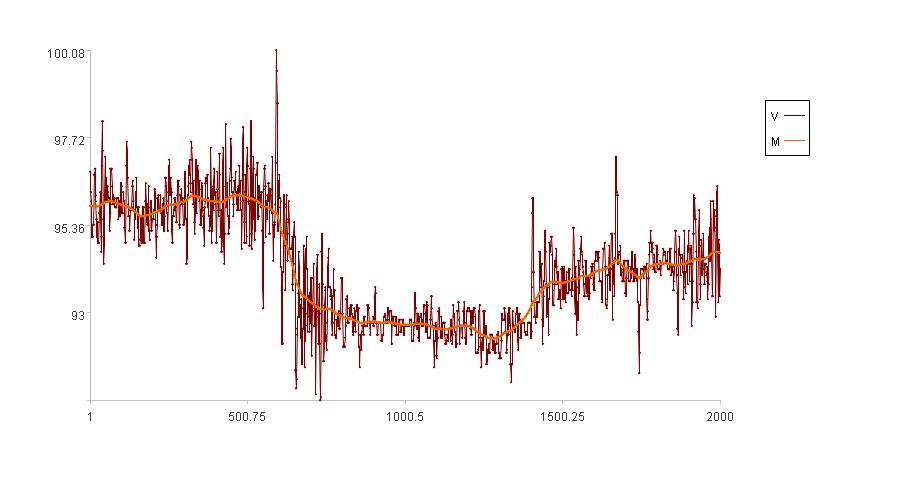
图中的“M”曲线是趋势线，它可以描述原值“V”的走势，而且实时性更强，有效避免了移动平均导致的延迟问题。

有了趋势线，再来思考问题二：如何识别工况？

工业生产中的工况非常多，为每一种工况设计一种数学方法不太现实，我们需要设计一个总体框架，在该框架下识别各种需要的工况。

参考积木的搭建思路，用几个简单的积木形状（如正方体、圆柱体等等）搭建出各种各样的形状（如城堡、飞机、人物等等）。我们也创建一些工况的基础特征，如升降特征、振幅特征等，用它们“搭建”出各种工况，如上升、下降、振荡发散等。

我们把曲线的基础特征总结成以下三类，每类又可以包含不同的指数：

1. 升降特征

升降指数：描述曲线上升或下降的情况，升降指数越大，上升趋势越明显；反之则下降趋势明显；当升降指数在0附近时，则曲线趋势为平稳。

2. 振幅特征

描述曲线振荡幅度的情况。

振幅指数：描述振动幅度大小，振幅指数越大，振动幅度越大；反之则越小。

振幅升降指数：描述振幅升降情况，振幅升降指数越大，振动幅度上升趋势越明显；反之则下降趋势明显；当振幅升降指数在0附近时，则振幅平稳。

3. 振频特征

振频指数：描述振动频率大小，振频指数越大，振动频率越大；反之则越小。

振频升降指数：描述振频升降情况，振频升降指数越大，振动频率上升趋势越明显；反之则下降趋势明显；当振频升降指数在0附近时，则振频平稳。

假设我们已经用数学方法算出这些特征指数了，怎么用他们识别工况呢？

以常见工况为例说明：

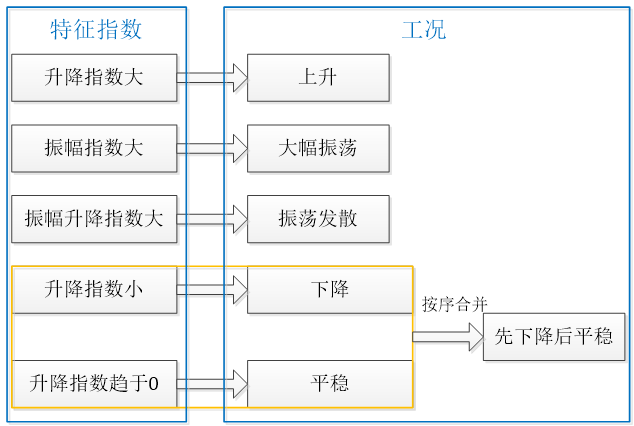
再回顾一下这张图：

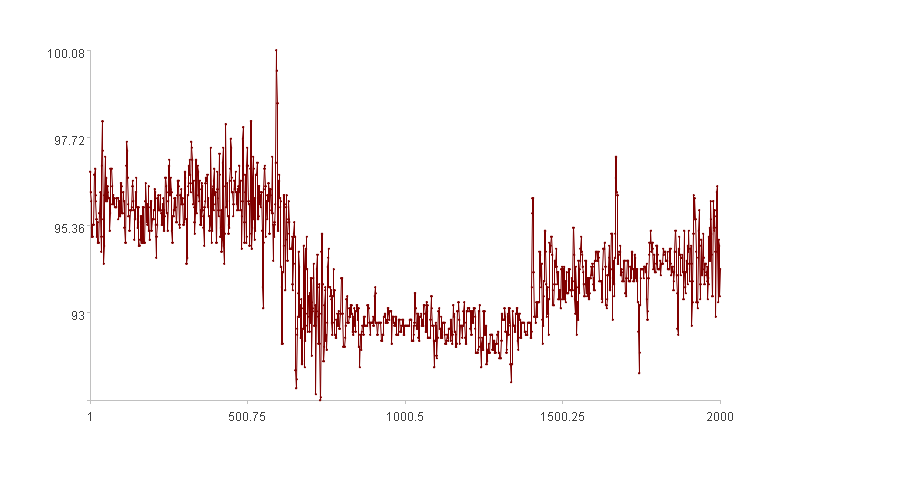
利用趋势线，三类特征指数都可以在它的基础上算出来，来看看他们的“样子”：

升降指数：

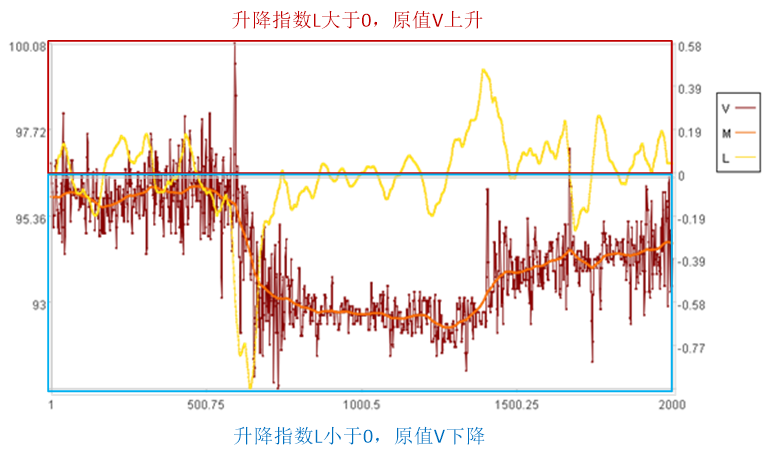
图中L是升降指数曲线。利用它可以快速识别上升和下降的工况。

振幅指数

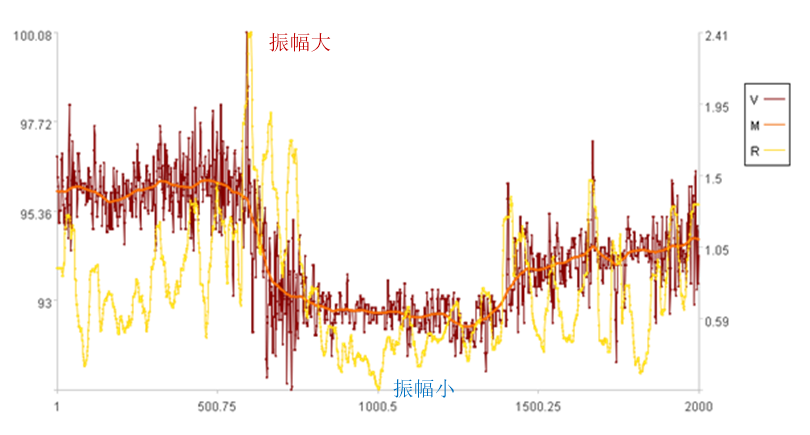
当原值偏离趋势线多时，振幅大；原值在趋势线附近时，振幅小。

振幅升降指数

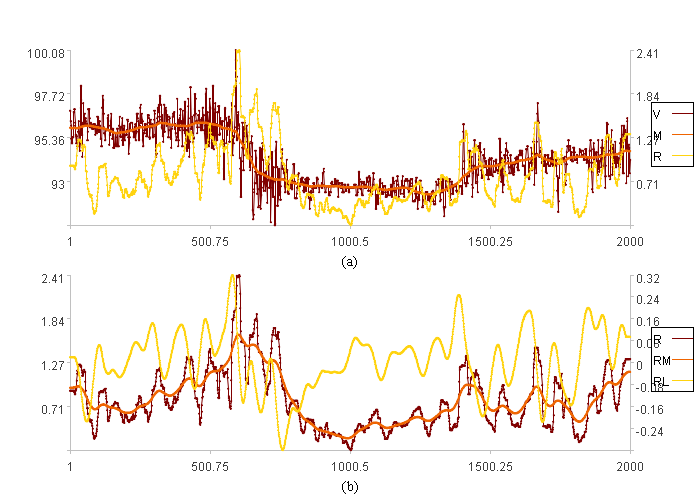
图(a)是原值V、趋势线M、振幅指数R的曲线图。图(b)是振幅指数R、振幅趋势线RM、振幅升降指数RL的曲线图。

振幅升降指数是描述振幅升降情况的指数，和升降指数描述原值升降情况一样，RL大于0，振幅上升，RL小于0，振幅下降。

振频指数

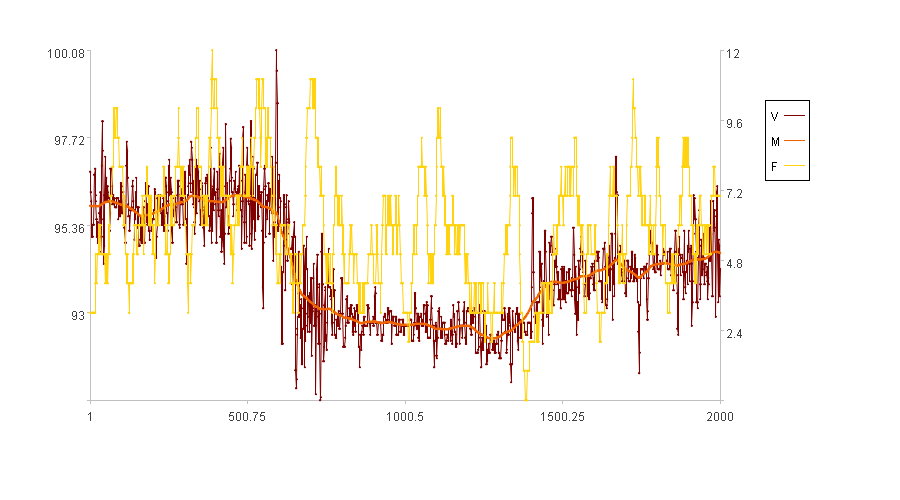
当原值穿越趋势线次数多时，振频大；原值穿越趋势线次数少时，振频小。

振频升降指数

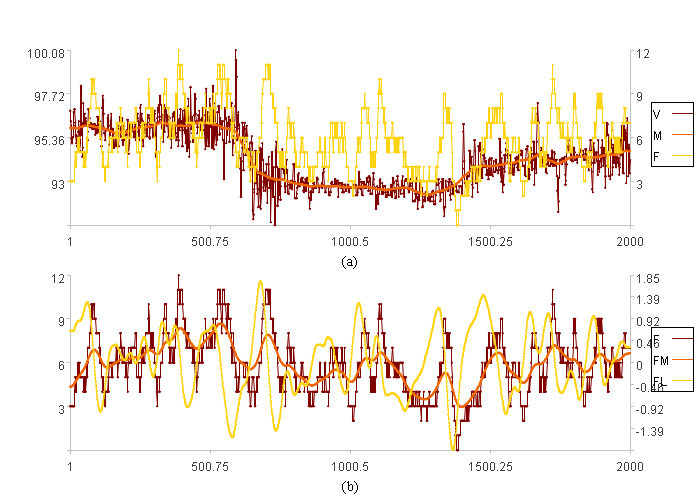
图(a)是原值V、趋势线M、振频指数F的曲线图。图(b)是振频指数F、振频趋势线FM、振频升降指数FL的曲线图。

振频升降指数是描述振频升降情况的指数，FL大于0，振频上升，FL小于0，振频下降。

特征指数计算出来了，如何筛选工况呢？

理论上只要筛选出各个指数的范围就可以了，但实际上这个范围很难设置，各个指数的数量级完全不同，下表是本例各个指数的数量级情况：

特征指数	数量级
原值	100
升降指数	0.1
升降速度指数	0.01
振幅指数	1
振幅升降指数	0.1
振频指数	10
振频升降指数	1

这样的指数没有办法设置合适的范围来筛选工况，需要把这些特征指数投射到一个固定范围内，在固定范围内设置参数即可，因为有些指数有正有负而且0本身有其特殊的含义，所以选择[-1,1]作为这个固定范围。

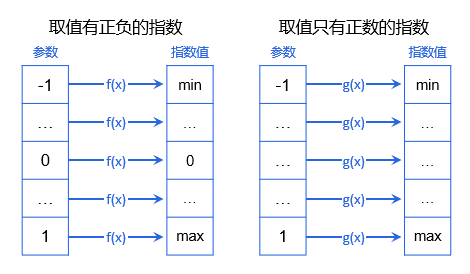
利用某种规则，将指数投射在[-1,1]内，参数只要在[-1,1]内设置即可完成工况筛选。

有时希望找出几段连续工况，如先下降后平稳，可以按下图流程筛选：

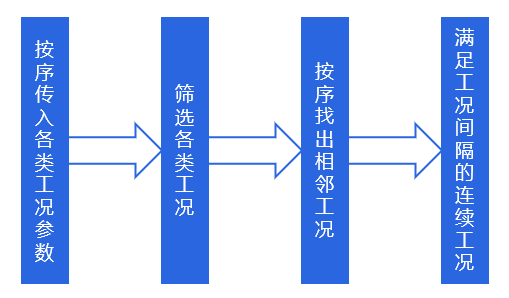
实践效果

把上面思路写成代码，就可以筛选工况了。

1. 筛选取值在[90,95]之间的工况。

根据原值范围筛选工况，不需要计算特征指数，也不需要投射，按照需求设置范围筛选即可。

SPL代码

	A
1	=file(“1Ddata.csv”).import@tc()
2	[Value]
3	[[90,95]]
4	[100,10000]
5	=A2.(~/">="/"number("/$[A3(]/#/$[)(1)]/")"/"&&"/~/"<="/"number("/$[A3(]/#/$[)(2)]/")").concat("&&")
6	=A1.pselect@a(eval(A5))
7	=A6.group@u(~-#)
8	=A7.select(~.len()>=A4(1)&&~.len()<=A4(2))
9	=A1.(Value)
10	=A8.(A9(~))

SPL提供了丰富的循环函数，简单的语句就能实现循环，为编码工作节省大量试错时间。

计算结果示例如下：

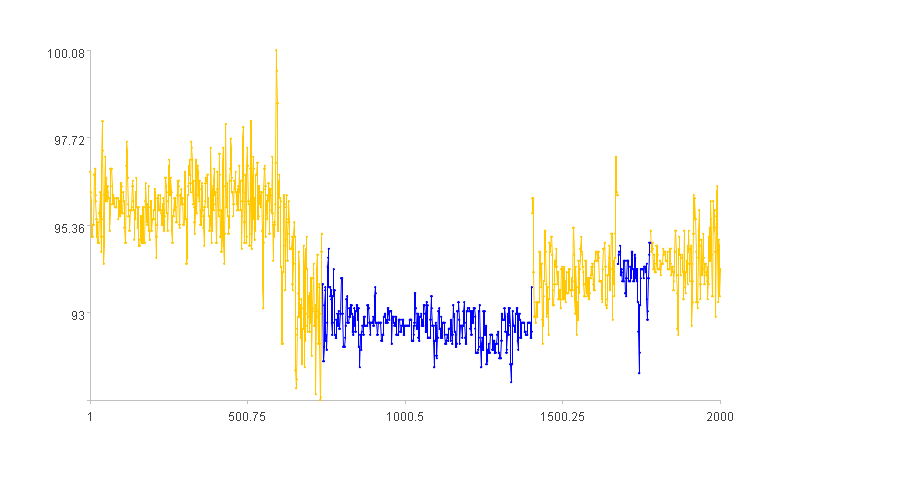
2. 上升工况

需要计算升降指数L，需要投射参数。

SPL代码

	A
1	=file(“1Ddata.csv”).import@tc()
2	600
3	[L]
4	[[0.1,1]]
5	[100,10000]
6	=A1.(Value)
7	=2*power(4,lg(A2/15,2)-1)
8	=fit_main(A6,A7)
9	=A2/40
10	=Lift(A8,A9)
11	=[A10.min(),A10.max()]
12	=[A11]
13	=A4.((idx=#,~.(arg_throw(~,A12(idx)(2),A12(idx)(1)))))
14	=A1.derive(A10(#):L)
15	=A3.(~/">="/"number("/$[A13(]/#/$[)(1)]/")"/"&&"/~/"<="/"number("/$[A13(]/#/$[)(2)]/")").concat("&&")
16	=A14.pselect@a(eval(A15))
17	=A16.group@u(~-#)
18	=A17.select(~.len()>=A5(1)&&~.len()<=A5(2))
19	=A18.(A6(~))

代码是示例性的，其中还调用了升降指数、参数投射等函数，这些函数并不是固定的，可以根据实际情况定义。

计算结果示例：

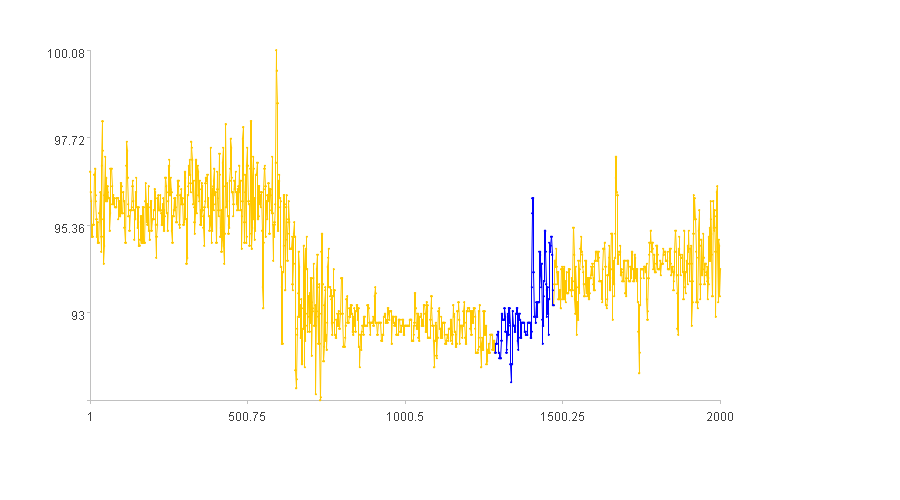
3. 振荡发散的工况

需要计算振幅指数R和振幅升降指数RL，需要投射参数。

SPL代码

	A
1	=file(“1Ddata.csv”).import@tc()
2	600
3	[VaL, VfL]
4	[[0,1],[-0.5,1]]
5	[100,10000]
6	=A1.(Value)
7	=2*power(4,lg(A2/15,2)-1)
8	=fit_main(A6,A7)
9	=A2/40
10	=A6--A8
11	=Amplitude(A10,A9)
12	=fit_main(A11,A7)
13	=Lift(A12,A9)
14	=VFre(A10,A9)
15	=fit_main(A14,A7)
16	=Lift(A15,A9)
17	=[A13.min(),A13.max()]
18	=[A16.min(),A16.max()]
19	=[A17,A18]
20	=A4.((idx=#,~.(arg_throw(~,A19(idx)(2),A19(idx)(1)))))
21	=A1.derive(A13(#):VaL,A16(#):VfL)
22	=A3.(~/">="/"number("/$[A20(]/#/$[)(1)]/")"/"&&"/~/"<="/"number("/$[A20(]/#/$[)(2)]/")").concat("&&")
23	=A21.pselect@a(eval(A22))
24	=A23.group@u(~-#)
25	=A24.select(~.len()>=A5(1)&&~.len()<=A5(2))
26	=A25.(A6(~))

代码结构和筛选上升工况的结构类似，都是计算特征——投射参数——筛选工况。

计算结果示例：

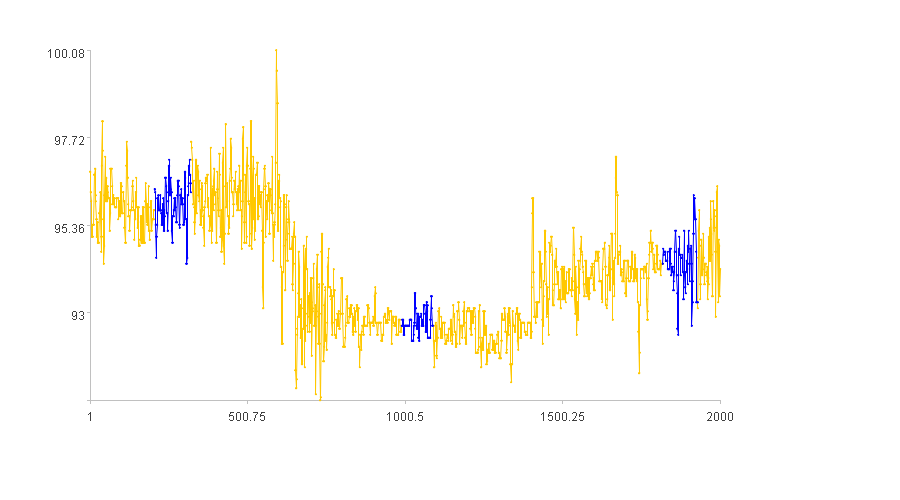
4. 先下降再平稳的曲线段

多段连续工况比单段的略显复杂，但思路是类似的，只不过把找到的两种工况按先后顺序合并起来。

SPL代码

	A
1	=file(“1Ddata.csv”).import@tcI()
2	=select_down(A1)
3	=select_stable(A1)
4	=[A2,A3]
5	=A4.conj((idx=#,~.new(~:seq,idx:seq_idx)))
6	=A5.sort(seq)
7	=A6.group@u(seq_idx-#)
8	=A7.select(~.len()==A4.len()&&(ss=~.(seq),ss(2)(1)-ss(1).m(-1)<=180))
9	=A8.((sq=~.(seq).conj(),to(sq.~,sq.m(-1))))
10	=A9.(A1(~))

SPL的集合运算能力很强，排序合并两种工况不在话下。

最后需要说明一下，本文只是介绍筛选工况的思路，特征指数只介绍了常用的升降、振幅、振频三类，在实际场景应用时可以根据情况增加其他特征指数，以便共同组合“搭建”出需要的工况。文中的代码也是示意性的，为每种示例写了相应的代码，实际上，可以只写一段通用的代码，根据不同的参数来识别不同的工况，当然代码会复杂一些，全部写出会占用过多篇幅，这里就省略了，有兴趣的读者可以和我们联系沟通。

开发这类算法常常需要做大量实验来选择合适的函数计算式并调整参数，SPL编程的高效性会发挥巨大的作用，在同样的时间内能够尝试更多种方案。