6.3 市值中性化
大部分因子当中都包含了市值的影响。所以当我们通过一些指标选择股票的时候, 每个因子都会提供市值的因素,选择的股票就会比较集中, 及选股的标准不太好。市值中性化就是排除市值影响后的因子。
计算方法:
回归法去除
建立目标因子 y 和市值 x 的回归方程,然后计算目标因子和其预测值之间的偏差,偏差就是不受市值影响的部分,即市值中性化后的结果
例如股票振幅,要计算市值中性化后的股票振幅,过程如下:
1. 获取两个因子数据,即股票振幅和市值数据
2. 对目标值因子股票振幅进行去极值,然后标准化
3. 建立市值 x 与股票振幅 y 的回归方程
4. 通过回归系数, 预测新的因子结果 y_predict
5. 求出目标因子 y 与 y_predict 的偏差即为新的因子值
以代码 600000 的股票数据为例,计算中性化股票振幅
| A | |
|---|---|
| 1 | =T(“D://600000.csv”).select( 收盘价 >0).sort(日期) |
| 2 | =A1.new(日期,( 最高价 - 最低价)/ 前收盘:amp, 总市值 ) |
| 3 | =A2.sert(2) |
| 4 | =A3(1).numnorm() |
| 5 | =A2.([lg( 总市值)].insert(0,1)) |
| 6 | =linefit(A5,A4(1)).conj() |
| 7 | =A2.derive(lg( 总市值)*A6(1)+A6(2):amp_pre) |
| 8 | =A7.new(日期,amp-amp_pre: 中性股票振幅) |
A2 获取股票振幅 amp 和总市值数据
A3 对 amp 去极值
A4 去极值后标准化
A5 构造最小二乘法拟合需要的矩阵 X
A6 最小二乘法线性拟合,返回拟合系数

A7 计算股票振幅的预测值
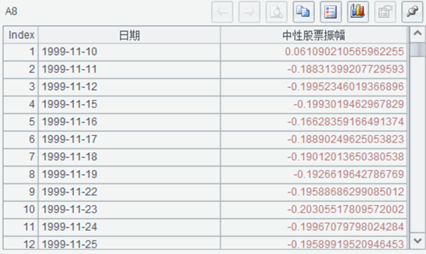
A8 计算股票振幅和预测值的偏差,即中性股票振幅