大表关联常常会出现性能问题。对于关联字段是主键或者部分主键的情况，SPL 提供有序归并算法来计算。

有序关联算法，要事先把这些关联表的数据按其主键排序。排序的成本虽然较高，但是一次性的。一旦完成了排序，以后就可以总是使用归并算法实现这种关联，性能可以提高很多。

如何实现有序存储，可参考SPL 的有序存储 。

有序归并关联

假设有 a、b 两个表，预先已经按照 id 有序存储。现在要按照各自主键 id 做内连接，用有序归并计算的原理大致是图 1 这样：

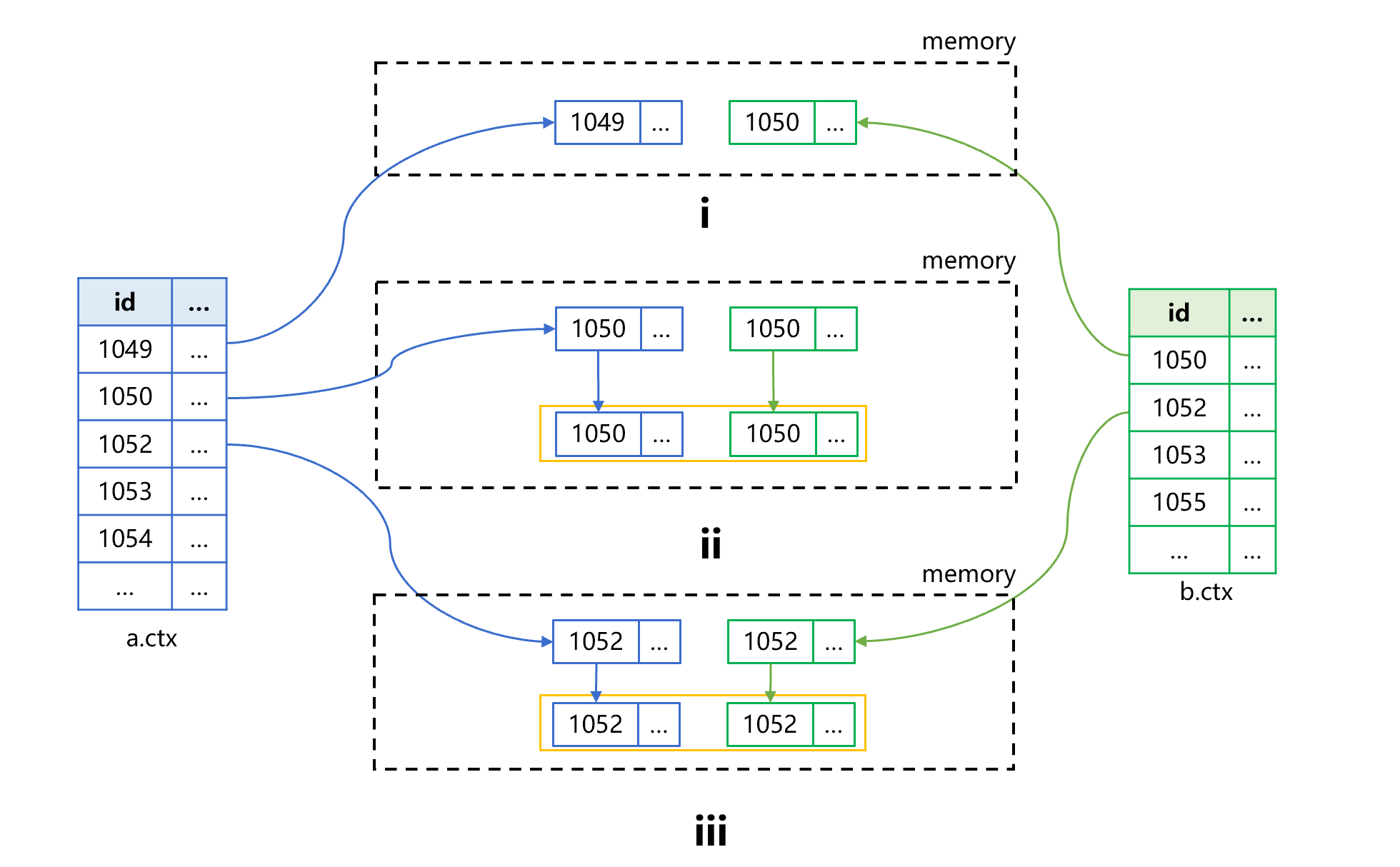
                                                                   图 1 有序归并做内连接

图 1 中，第 i 步从 a、b 两个表中各读取一条记录到内存中，判断 id 的大小关系。这时 a 表中的 id 是 1049 小于 b 表的 id1050。第 ii 步，舍弃掉 1049 这条记录，再从 a 表中读取一条记录，发现两个 id 相等，都是 1050。将两个记录作为字段，生成内存结果表的新记录。第 iii 步，从 a、b 中再各读取一条记录，判断 id 的大小关系，这时都是 1052，可以直接生成内存结果表的新记录。

接下来，继续从 a、b 中再各读取一条记录，判断 id 的大小。如果有一个表取出的 id 比较小，则舍弃掉，在这个表中再读取记录。直到出现 id 相等，生成内存结果表的新记录。

这样，不断读取数据，不断判断大小、生成新记录，就构成了一个循环。直到 a、b 其中有一个数据读取完毕，循环就可以结束了。这个循环大致是下图 2 这样：

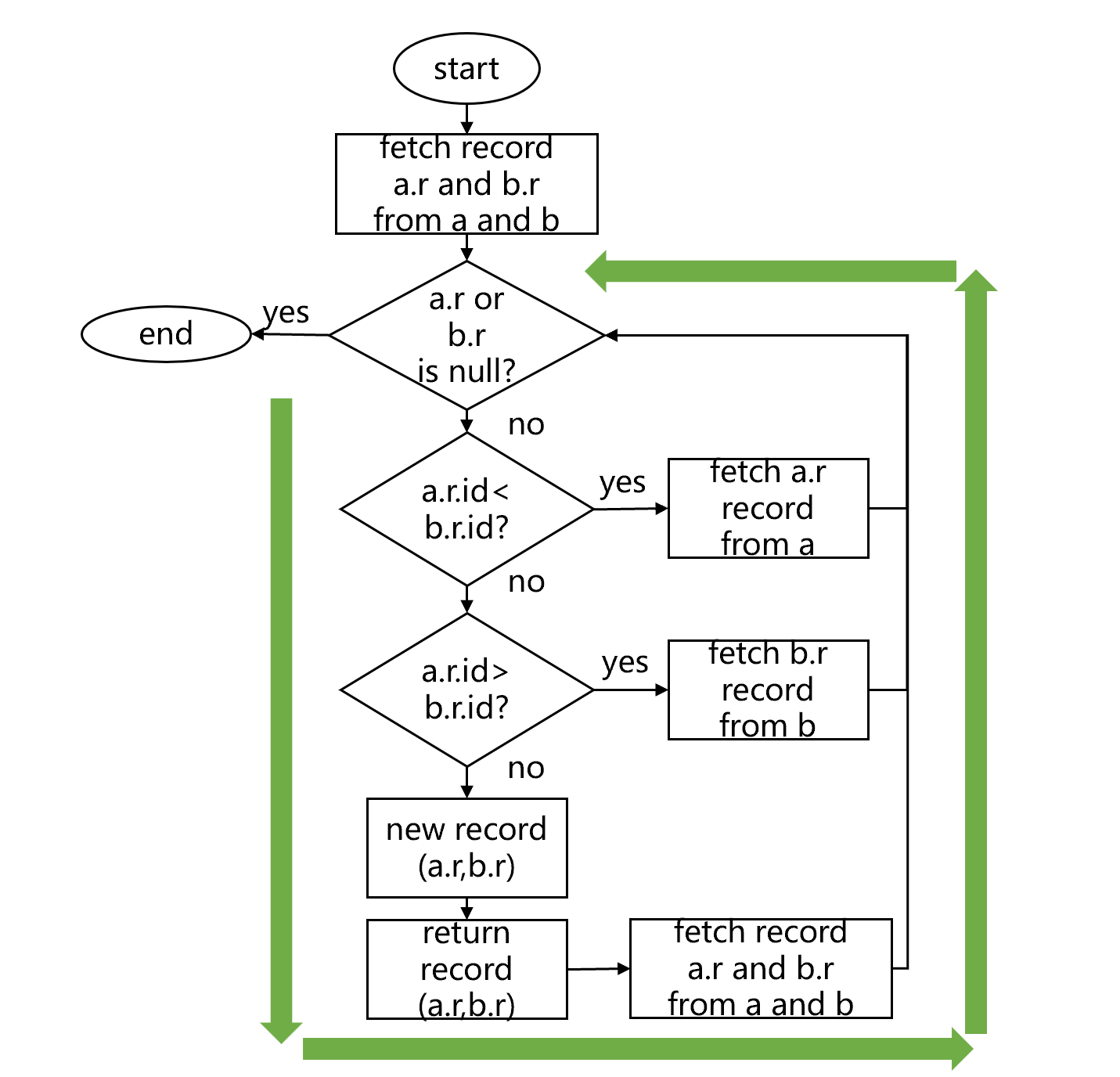
                                                                   图 2 有序归并内连接的循环

SPL 将这个循环封装成一个延迟游标，通过控制循环的执行和暂停，给游标的调用者分批返回关联结果。

全连接和左连接也可以采用和内连接类似的算法实现，调整中间判断方法即可。同样也可以推广到 n 个表的情况。关联字段是 a 表的主键，是 b 表的部分主键时，算法原理也是类似的，只要循环最后返回结果后，只 fetch b.r 即可。

有序归并算法只要把两个表都遍历一次就可以完成，即使是大数据表，也不必借助缓存文件。如果两个表的规模分别是 N 和 M，则复杂度为 O(N+M)。无序时实现连接运算，不做优化时要两两比较，复杂度将会是 O(N*M)，远远大于 O(N+M)。数据库通常使用的是哈希分堆算法，复杂度一般也会远大于有序归并算法。而且对于大数据的外存运算，哈希分堆还会产生缓存文件的读写动作，以及哈希函数可能出现的运气不好的情况。利用有序后的归并算法有巨大的性能提升。

SPL 用 joinx 函数实现连接运算的有序归并算法：

无选项、@1、@f 的 joinx 函数分别表示内连接、左连接和全连接。

joinx 会假定作为参数的游标已经有序，针对无序游标执行这两个函数会得到错误的计算结果。

同步分段并行

有序归并算法要将数据一条条的从两个（或更多）游标中读出后比对，这种逻辑下无法直接实现分段并行。这是因为，直接分段是按记录条数将表尽量平均分段，无法保证两个表的关联字段在对应分段中能同步分布。例如，将 a 表、b 表直接分为 4 段，类似下图 3 这样：

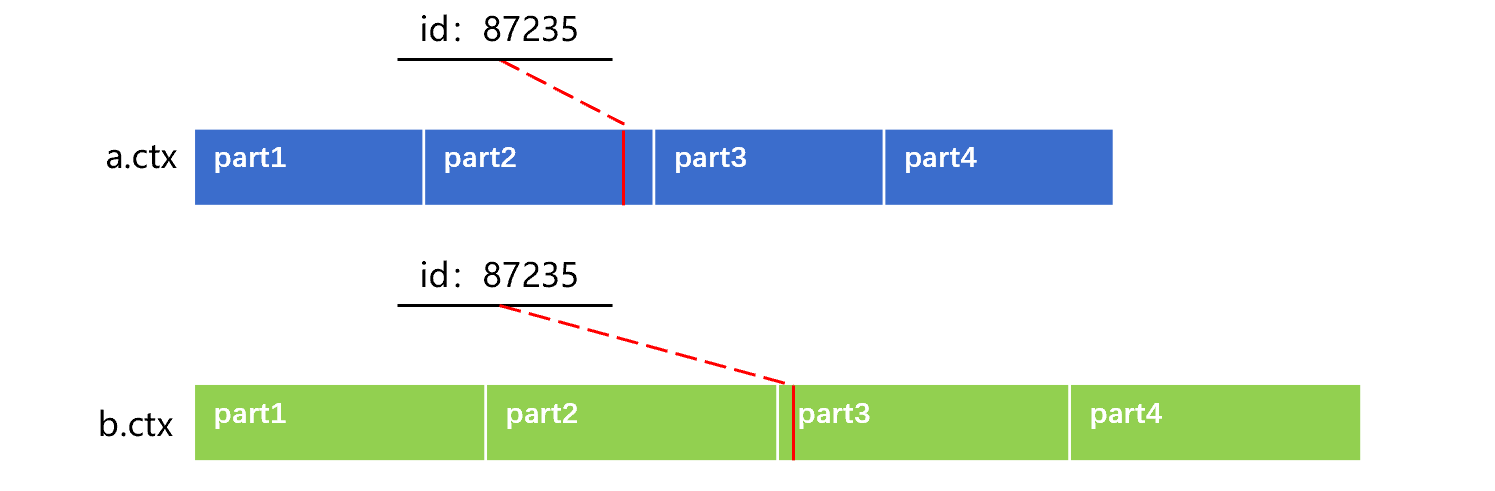
                                                                   图 3 直接分段

图 3 中，a 表在第二段 id=87235 的记录，会对应到 b 表的第三段上，出现了不同步的问题。

SPL 再次利用主键的有序性解决同步分段问题。例如，将 a 表、b 表同步分为 4 段的做法大致是下图 4 这样：

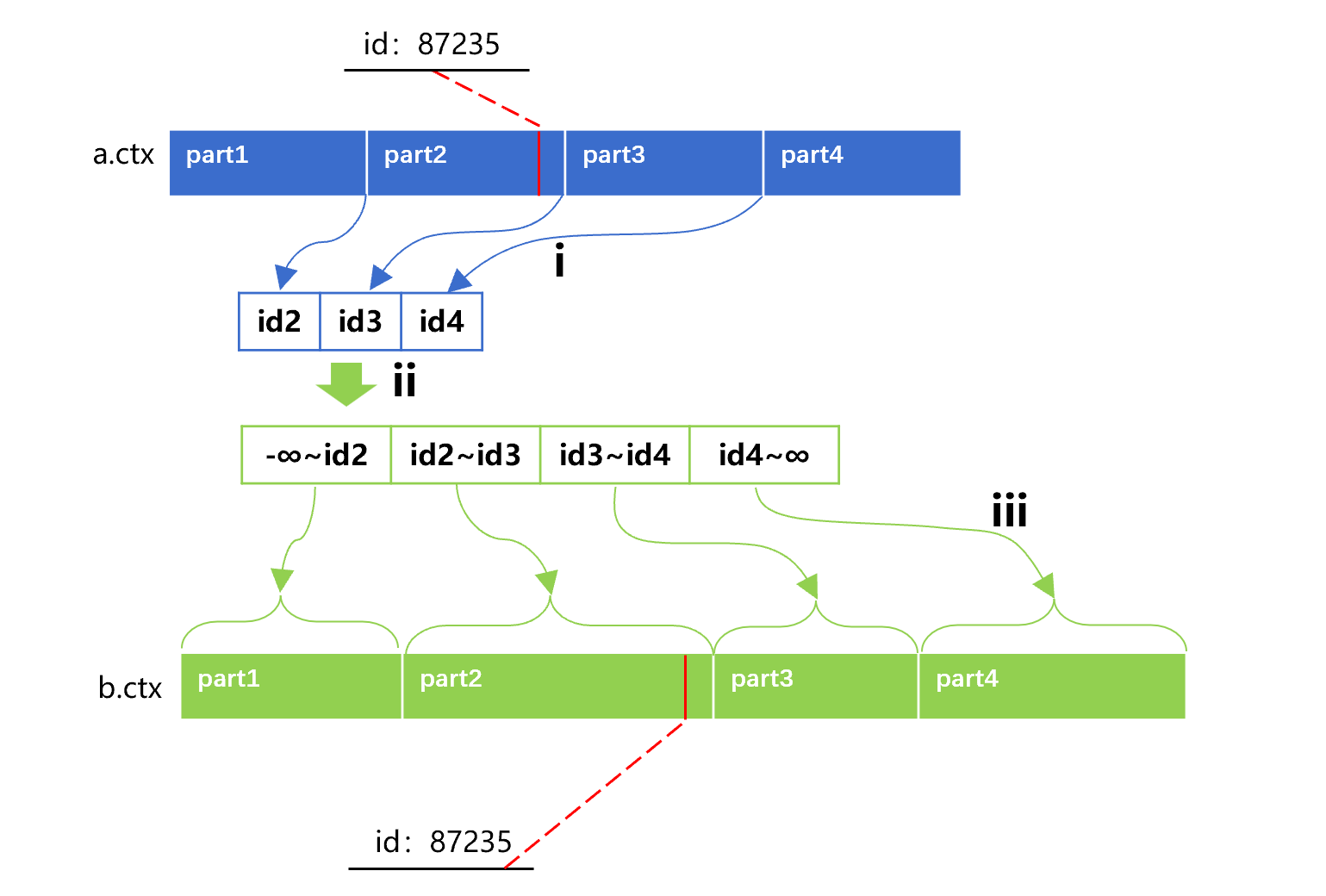
                                                                   图 4 同步分段并行

图 4 中第 i 步，将 a 表直接分成 4 段。因为 a 表对 id 有序，所以可以快速取出每一段第一条记录的 id 值。第 ii 步，用这些 id 值拼出 b 表 id 的四个区间条件。由于 b 表也是主键有序的，主键值落在这些区间的记录是连续存储的，也可以迅速地被定位并生成游标。第 iii 步，在并行计算时，每个线程中 a 表仍然直接分段，b 表则用相应的区间条件来分段，这样就能保证两边的主键值是同步对应的，得到分段游标的关联游标再继续计算。

以上面讲过的 id=87235 的记录为例，这时仍然在 a 表 part2 中，也就是说在 id2 到 id3 之间。而 b 表中，所有 id 值在 id2 到 id3 之间的记录都在 part2 中，所以 id=87235 的记录一定也在 b 表的 part2 中，不会出现不同步的问题。

SPL 提供了相应的函数用这种方法生成可关联的多路游标：

A2 中正常生成 a 表的多路游标，B2 中可以基于 A2 生成 b 表的多路游标，因为组表在创建时可以定义主键（create 时带 #的字段名），这里就不用再写字段名而直接会将两个表的主键对应来查找（两表的主键字段名可以不同）。A3 的 joinx 也会返回多路游标。

SPL 也支持在有序的集文件和文本文件上使用这种对位同步分段机制，但需要写上关联的字段，工作原理是一样的，这里就不举例了。

需要注意的是：主键是不重复的，分段时不可能把两个相同主键的记录分到两个段中。但 a 表主键关联 b 表部分主键时，b 表的关联字段并不是全部的主键，可能有重复值，也就可能在两个直接分段中出现关联字段相同的记录。所以，在这种情况下做并行分段时，要以 a 表作为基准，b 表跟随 a 表分段，而不能随意倒过来。