索引类似于原表的 "目录"，是在原表之外，另外建立的存储结构。在做查找计算时，先查索引，在 "目录" 中找到原表的位置，再去原表找到对应的记录。查索引比查原表快的越多，索引提速的效果越明显。

建立索引是个相对独立的过程，可以放在系统初始化时一次性建成，定时更新。我们这里介绍 SPL 的内存索引。

位置索引

有时候，为了完成和顺序相关的计算，我们要将内存数据表按照某个字段有序存储。这种情况下，如果还想利用其他字段有序来优化性能，就比较困难了。

比如，订单表包含字段客户号、时间和其他字段。数据按照时间先后有序存储，这样可以方便的计算相邻两个订单的间隔时间。要实现的计算需求是，查找指定客户号的第一个订单，再计算这个订单和相邻下一个订单的时间差。

如果能找到指定客户号的记录在订单表中的位置，则只要再找出下一条记录来计算时间差即可。但订单表没有按客户号排序，不能使用二分法，只能顺序查找，所以会很慢。如果把数据按客户号排序了，又会丢失时间先后的位置信息。

 

SPL 提供的位置索引算法，可以解决这个问题。首先建立订单表的位置索引。为了便于理解，假设订单表只有 10 条记录，存储的位置序号（index）为 1 到 10。订单数据按照时间 otime 字段有序，对客户号 cid 是乱序的，如图 1 中最左边的 orders 表：

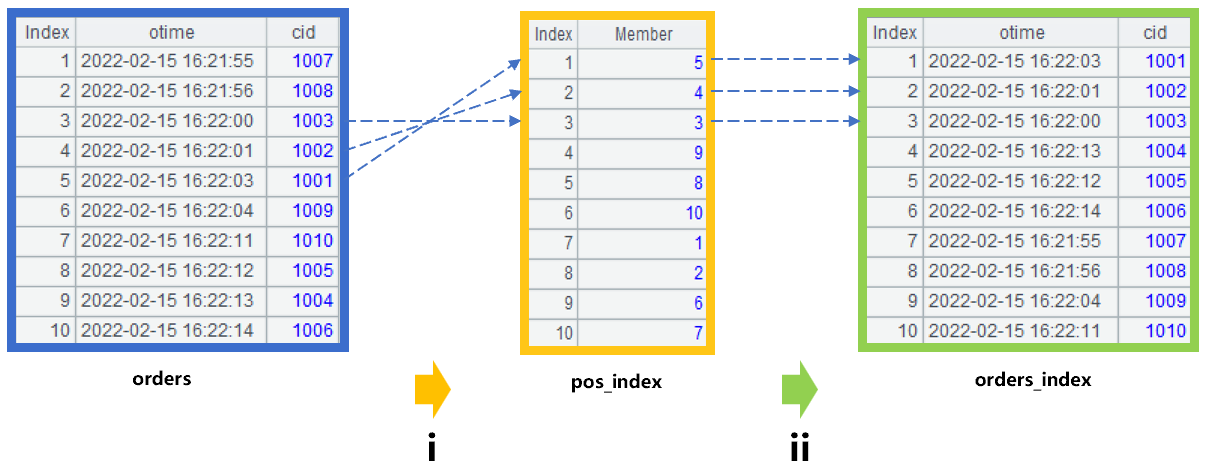
                                                                  图 1：建立位置索引

 

图 1 中的第 i 步，是建立位置索引 pos_index。其 10 个成员，是 orders 按照客户号 cid 升序排序结果，在 orders 中的位置序号 index。比如 pos_index 的第 1 个成员，对应 orders 表中 cid 最小的记录。在 orders 表中找到 cid 最小的记录，其 index 为 5，因此 pos_index 中第 1 个成员的值就为 5。同样的道理，第二个成员值为 4。以此类推，计算出 pos_index 中的所有成员。

图 1 中的第 ii 步，是建立 orders 的排序表 orders_index。其成员是先找到 pos_index 相同成员的值，再以这个值为序号，从 orders 表中取得的记录。比如：pos_index 第 1 个成员值为 5，就从 orders 中找到第 5 条记录，作为 orders_index 的第 1 个成员。这样生成的 orders_index 实际上就是 orders 按照客户号 cid 排序后的结果了。需要注意的是，orders_index 并没有将 orders 的记录复制一遍，而是存储了记录的地址，可以减少内存占用。

 

索引建立之后，我们就可以利用索引实现查询需求了。假设需要查询的客户号 cid 是 1009，计算的过程可以用下图 2 来示意：

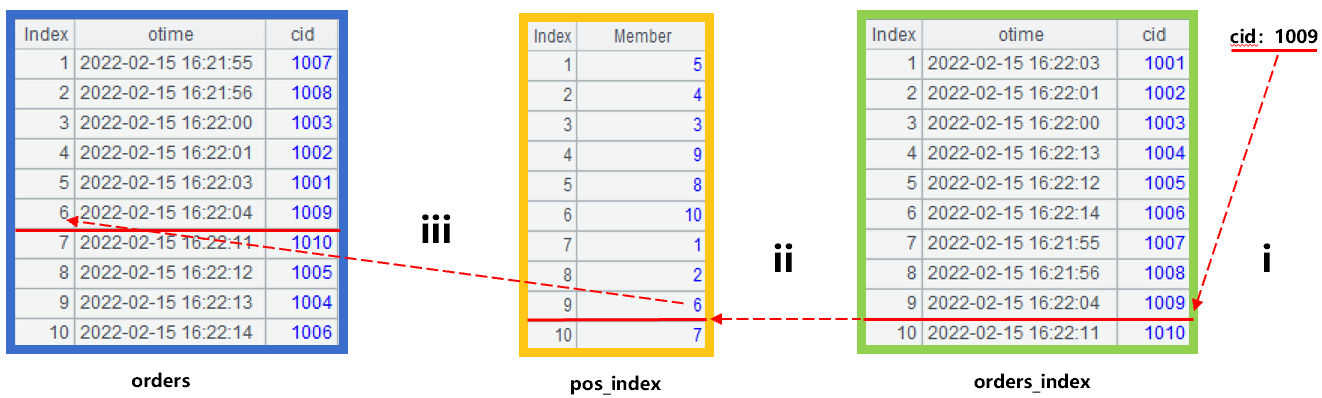
                                                                  图 2 利用位置索引完成查找

图 2 中的第 i 步，在客户号 cid 有序的 orders_index 中，用二分法查找 cid 为 1009 的记录，得到其序号为 9。第 ii 步，在 pos_index 中找到序号也是 9 的成员值为 6，也就是说 1009 在 orders 中对应的序号是 6。第 iii 步，在 orders 中找到序号为 6 的记录，取其 otime 和下一条记录的 otime 求时间差，就是我们需要的结果。

 

第 i 步是二分法查找，第 ii、iii 步是位置定位查找，三个步骤的总体复杂度和二分法相当。比直接在 orders 上做顺序查找要快很多。

 

SPL 实现上述计算的代码，大致是这样的：

	A	B
1	=file("orders.btx").import@b(otime,cid  )
2	=A1.psort(cid)	=A1(A2)
3	=B2.pselect@b(cid:1009)	=A1.calc(A2(A3),otime[1]-otime)

A1：读入按照 otime 有序的 orders 表。

A2：对应图 1 第 i 步，建立位置索引 pos_index。

B2：对应图 1 第 ii 步，建立排序表 orders_index。

A3：对应图 2 第 iii 步，用二分法查找 cid 为 1009 的记录位置。

B3：其中的 A2(A3) 对应图 2 第 ii 步，在位置索引中找到原表 orders 中的位置。其他对应图 2 第 iii 步，完成计算。

A1、A2、B2 是加载数据并建立位置索引的过程，结果可以复用。在系统初始化时计算一次即可，后续查找时就不必每次都计算了，进一步提高性能。

 

实际测试证明了位置索引在性能上的优势。在相同数据量和计算环境下，使用位置索引后，计算速度提升了 80 倍以上。对比测试详细情况参见：性能优化技巧 - 位置利用。测试结果是这样的：

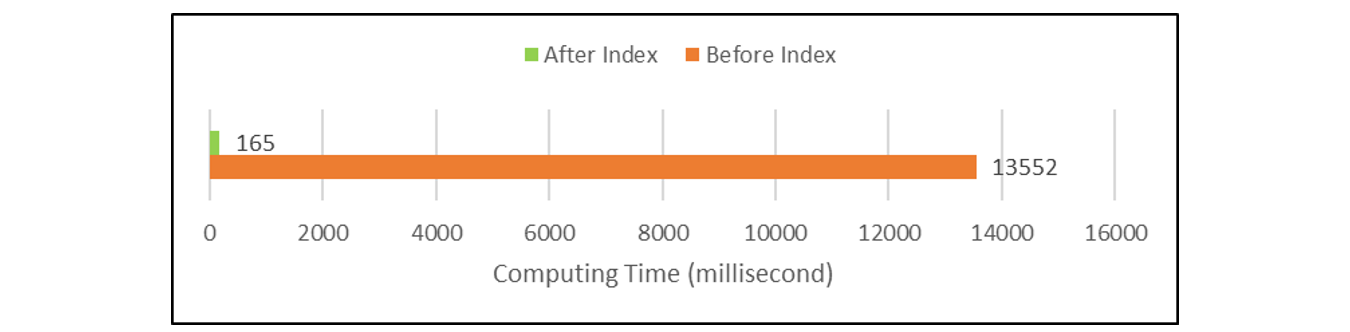
                                                                  测试结果图 1：位置索引对比测试

哈希索引

使用某个函数将被查找字段值计算成一个 1 到 M 之间的自然数，称为该记录的哈希值，此函数称为哈希函数。将内存表的记录按哈希值分组后，可得到一个长度为 M 的两层结构 H（其中可能有空成员），称为哈希索引。哈希索引的第一层是 1 到 M 之间的自然数，第二层是原表记录组成的子集合。哈希索引没有将原表的记录复制一遍，而是存储对应记录的地址，可以减少内存占用。

在查找字段的指定值时，先计算其哈希值，再按序号定位到哈希索引中相应的分组子集，然后在这个分组子集中使用顺序或二分查找方式进一步找到目标记录。

例如，用户表包含 id 和用户名（name）等字段，我们采用经常用于整数字段的取余数方法作为 id 的哈希函数。为了便于理解，假设用户表只有 10 条记录，如图 3 中最左边的 users 表：

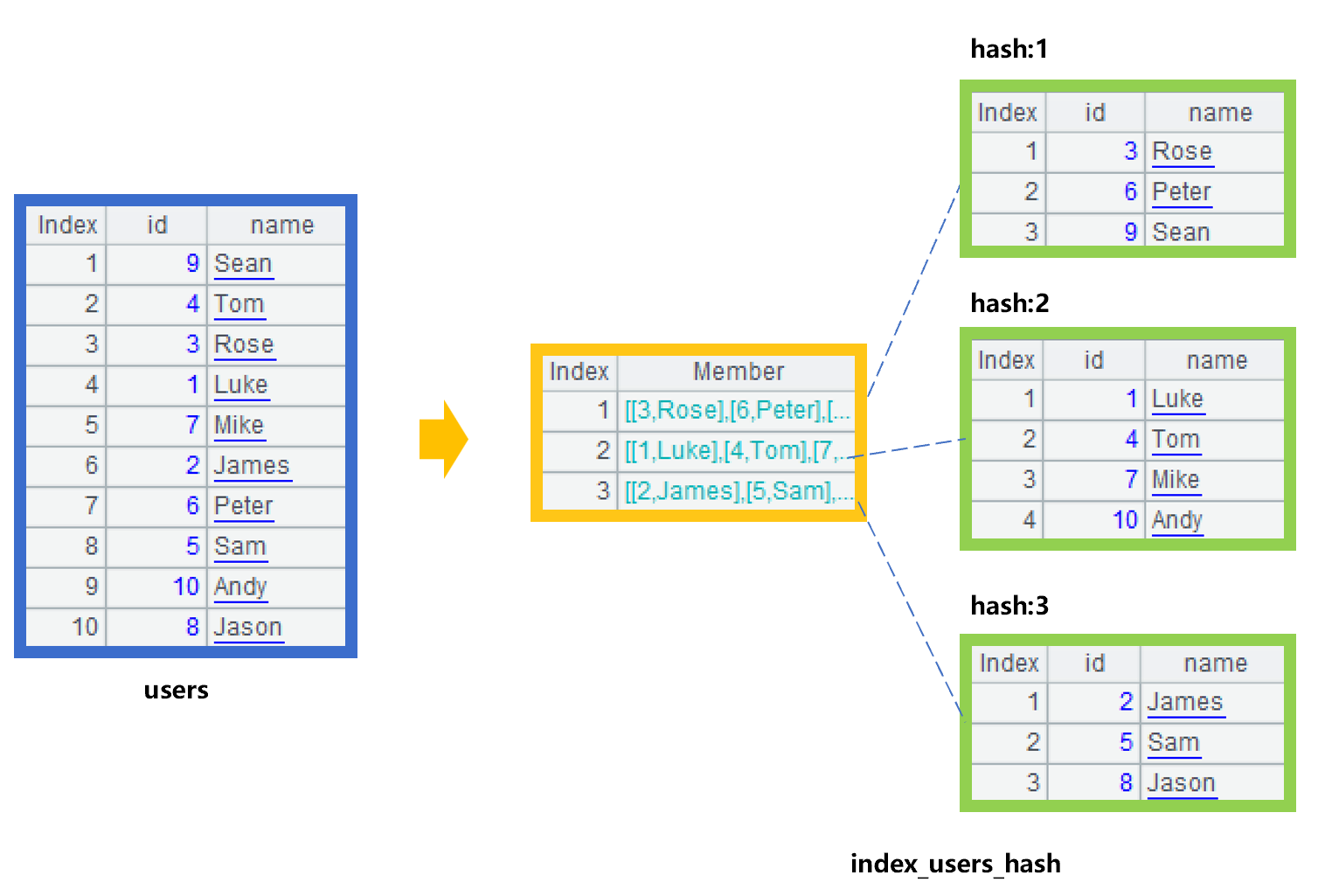
                                                                  图 3 建立哈希索引

对 users 表的 id 字段，计算 id%3+1 得到的哈希值是 1、2 或 3。按照每条记录的哈希值，分别存入对应的分组子集，生成哈希索引。这里的分组子集中，数据按照 id 有序，在组内查找时可以采用二分法提速。

 

建立了哈希索引，就可以用于 id 字段的查找了。设我们要查找 id 为 7 的用户。大致过程如下图 4 所示：

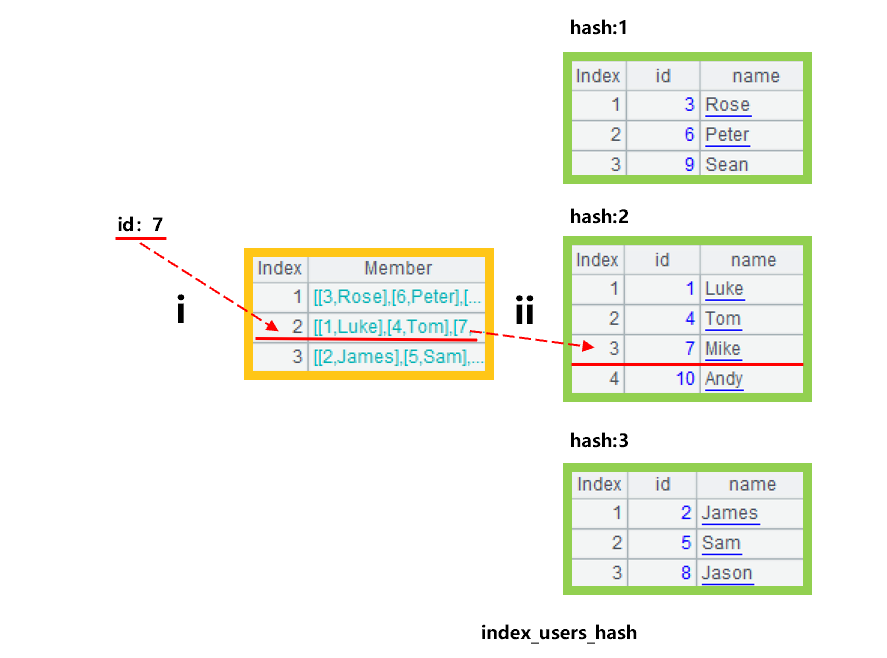
                                                                  图 4 利用哈希索引完成查找

第 i 步，先用哈希函数计算 id 值 7 的哈希值为 7%3+1 等于 2，确定要找的记录在第 2 个分组子集中。第 ii 步，在分组子集中，用二分法查找 id 为 7 的记录。如果分组子集中数据没有按照 id 有序，这里就要顺序查找了。

 

这个例子中，我们将 10 条记录分成了三组。查找时，先按序号定位，再二分查找。在分组子集中查找的数据量只有总数据量的三分之一。这个例子是运气比较好的，哈希索引的三个分组数据量比较平均。也有运气不好的时候，比如 id 值的余数绝大部分是 1、2，那么三个组的数据量就很不平均了。

 

一般的，设总数据量为 N。运气好的时候，哈希索引每个分组子集数据量都接近 N/M 个，由于哈希值计算和序号定位查找的复杂度为 O(1)，则建立哈希索引后的查找复杂度将降低 M 倍，和查找长度为 N/M 的内存表相当。如果运气不好，哈希索引各分组子集的成员个数分布很不平均，哈希索引在极端情况时有可能并不会提高性能，这取决于哈希函数的设计和原数据集中被查找键值的分布情况。

 

不过，运气通常不会太差，哈希索引大多数情况都会获得较好的性能提升，甚至能在原数据无序时，比先排序再使用二分法更有优势。

 

哈希索引的缺点在于需要占用内存空间来保存这个索引，而想速度更快，就需要更大的索引，也就会占用更大的空间。

 

SPL 提供了针对主键的哈希索引，会自动使用系统内置的哈希函数。

	A	B
1	=file("users.btx").import@b(id,name  )
2	=A1.keys@i(id)	=A2.find(12345)
3	=A1.keys@i(id;100)	=A3.find(12345)

A2 在设置主键时用 @i 可以同时建立索引，在 B2 find 查找时如果有索引将会自动使用。A3 在建索引时用参数控制了哈希索引的长度（即 M 值）为 100，SPL 程序员可以根据实际情况来调整。

过滤后索引复用

很多时候，内存数据表会先做过滤，再进行其他计算，比如关联、分组等等。如果数据表已经建立了索引，那么过滤之后原来的索引就不能用了。如果进一步计算需要用到索引的话，就要重建。而建索引是需要时间的，要计算主键哈希值等等。在过滤之后的记录数仍然比较多时，建索引时间也不小，而且因为过滤条件不可预测，这个索引也不能事先准备。

SPL 提供过滤后索引复用的机制，直接将原表索引中不符合过滤条件的记录删掉，就可以给过滤的结果使用了。

以用户表的哈希索引为例，过滤出用户名不是 Peter 也不是 Tom 的用户之后，索引复用的过程大致可以用图 5 来表示：

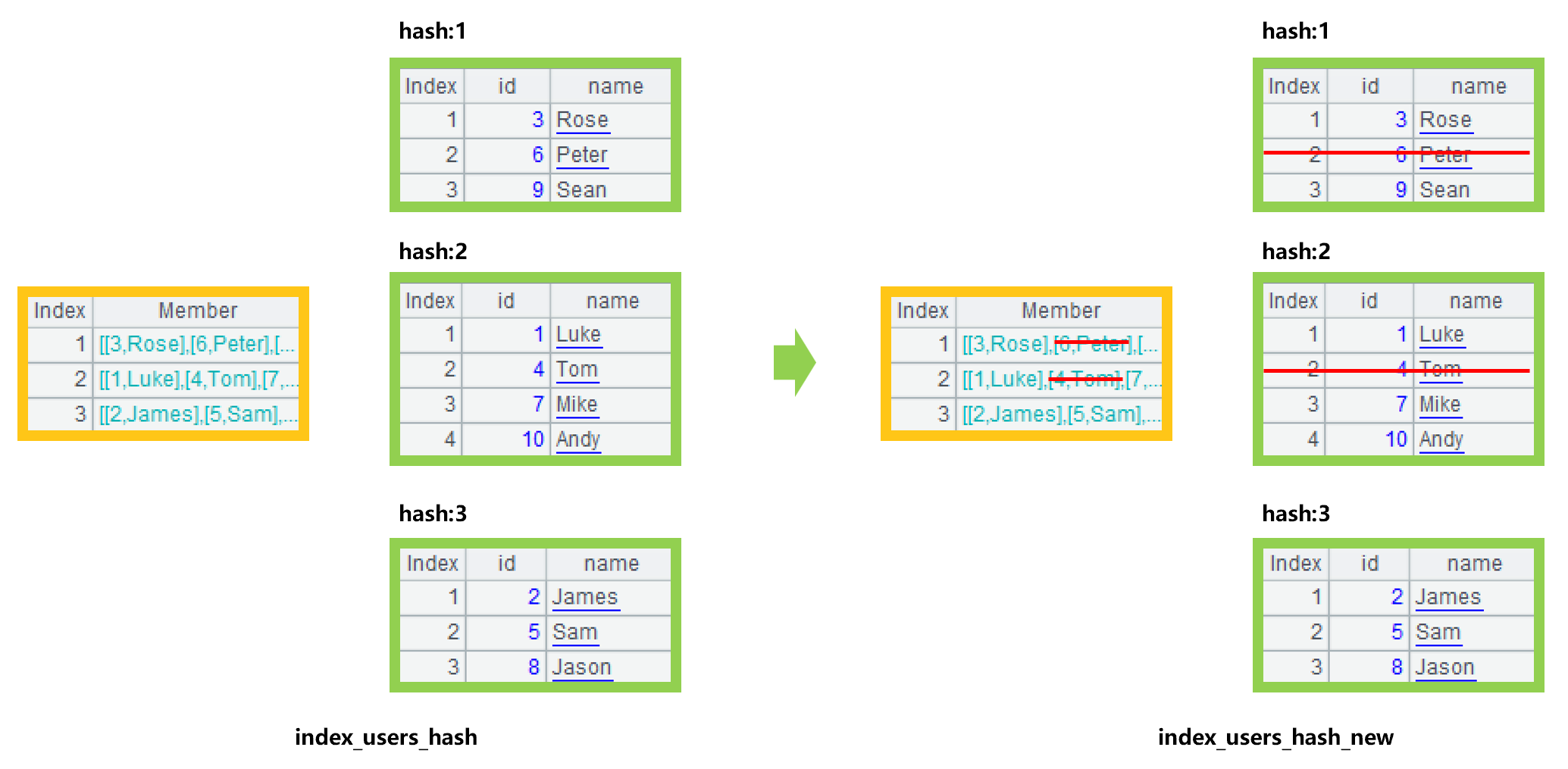
                                                                  图 5 过滤后索引复用

图 5 中，用户表的索引删除 Peter 和 Tom 的记录后，直接生成了过滤结果的新索引，省去了新建索引的时间。但是，我们也发现，如果过滤掉的记录数很多（剩下的较少），删除索引中记录的动作也不会很快。所以，剩下记录较少时，重建索引很可能更快。具体采用哪种方式，要根据实际情况决定。

 

SPL 的过滤后索引复用的代码写法大致如下：

	A
1	=file("users.btx").import@b(id,name  ).keys@i(id)
2	=A1.select@i(name!="Peter"   && name!="Tom")
3	=A2.find(9)

A2 中用 select@i 采用了过滤后复用索引的机制，过滤结果带主键索引。

A3 中在查找主键时，就利用了新建的索引。

多层序号索引

SPL 提供序号定位算法，在【性能优化】1.2 [内存查找] 序号定位有说明，这里做个简单介绍。如果被查找字段的取值，正好和记录在内存数据表中的位置相同，就可以直接用指定的字段值去数据表中取对应位置的记录。

例如：用户的 id 字段是从 1 开始的连续自然数，数据按照 id 有序存储在内存的用户表中。如果要查找 id 为 12345 的用户，直接从用户表取得位置为 12345 的记录即可。使用序号定位不需要进行任何比对，查找的复杂度为 O(1)。而且序号定位不用在原表之外建立索引。

 

但是，有些情况下，序号定位就不适用了。比如中国公民的身份证号，由一串数字构成，本身就可以理解成一个自然数，天然是一种序号，但我们并不能把身份证号按自然数对齐再使用序号定位来查找。

 

这是因为，序号定位要求一个长度不小于最大序号的序列来存储所有待查找记录和用于填补空缺的 null 值，如果直接把身份证号转换成自然数，其序号范围会大到当前计算机内存无法承受的地步（10¹⁷，身份证号共 18 位，最后一位校验不算），要填入 null 的序号数量远远多于有记录的序号。这种时候就无法直接使用序号定位了。

 

针对这种情况，SPL 提供了多层序号定位和排号键索引算法。以身份证号查找人员为例，我们要利用人群具有的共同特征，让身份证号分布相对集中，而不会布满所有 18 位自然数构成的范围。利用这个特征，可以构造多层序号定位方法以减少实施序号定位时占用的空间。

例如，地区为北京市，出生日期在 2016 年到 2018 年之间的人群，由于生日和地区都比较集中，我们可以建立下图 6 这样的三层序号索引：

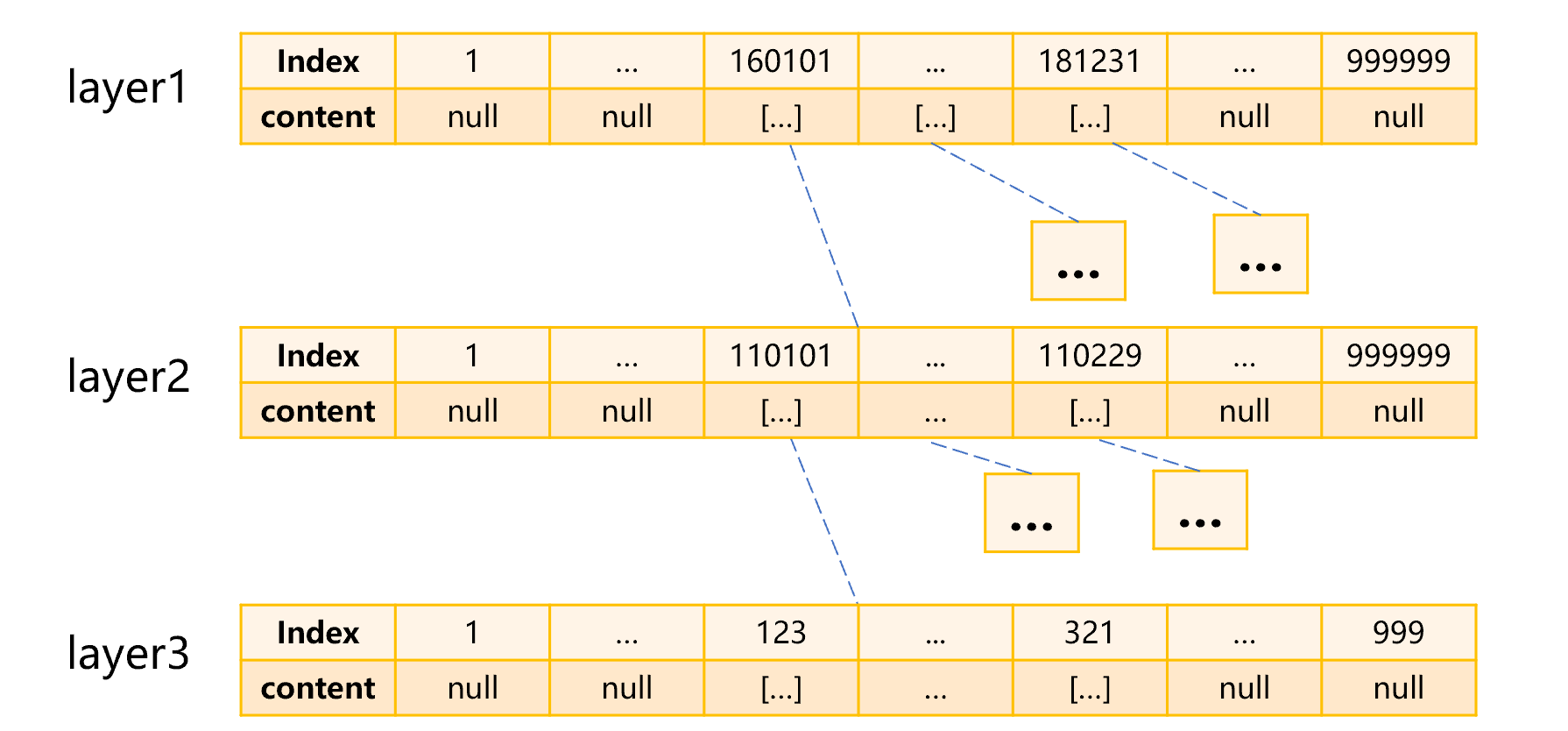
                                                                  图 6 建立多层索引

第一层是出生日期。年份只要看后两位即可，不会有重复，所以我们可以将日期看作最大值为 999999 的连续自然数。也就是将身份证号按照出生年月日分到 999999 个分组子集中。比如 2016 年 1 月 1 日出生的身份证号就分到 160101 这个位置的分组里。2016 年到 2018 年的日期有 1000 个左右，所以第一层只有 1000 个非空成员，其他都是空。

第二层是地区。是将每个日期的身份证号，按照前 6 位（地区编号），分成 999999 个分组子集。第一层为空的成员是没有第二层成员的，所以第二层的成员总数大约是 1000*999999 个。北京市只有大约 20 个地区，所以第二层的非空成员有约 1000*20 个。

第三层是身份证号后 3 位，不包括校验位。根据第一、二层非空成员的个数，第三层大概有 1000*20*999 个成员。

这样三层的成员数加起来就是 999999+1000*999999+1000*20*999，总数大约是 1G 多，占用空间是几个 G 或者 10 几个 G，现代计算机是可以装下的。

 

从图 6 可知，SPL 把多层索引看成一个树状结构，如果数据满足前述的分布集中的特征，那么看上去这个树会有大部分树枝延伸不到最深的层次，而在较浅的层次就中断了，也就不再占用空间。整个树占用的空间有可能很小，小到内存可以放得下的地步。

多层序号定位只能在分层后前几个层次中空值很多的情况下使用，如果空值较少甚至没有空值，多层序号结构占用的空间比单层还要更大。

 

建立了多层索引，就可以用于查询指定的身份证号了。比如要查询 110101201601013212，查找的过程大致是图 7 这样：

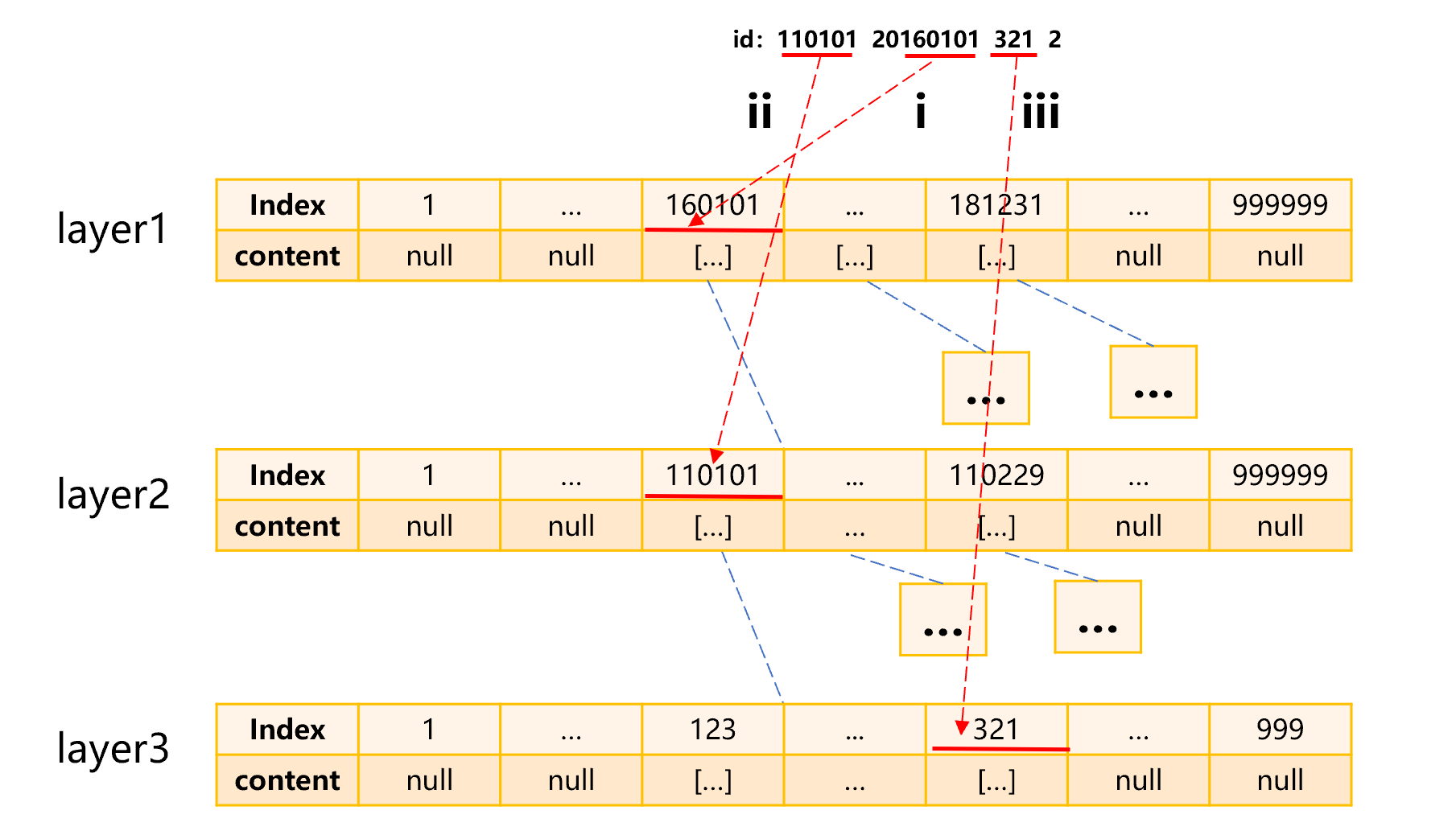
                                                                  图 7 利用多层位置索引查找身份证号

图 7 中第 i 步，利用出生日期的后 6 位 160101，在第一层索引的 160101 位置找到第一层分组子集。第 ii 步，在这个分组子集中，利用身份证前 6 位 110101 找到这个位置的第二层分组子集。第 iii 步，再在这个分组子集中，利用身份证最后 3 位（不包含校验位）321 找到第三层分组子集。最后，在第三层分组子集中查找身份证号就可以了。

 

多层序号使用条件比较复杂，在层次较多或生成排号键的运算较复杂时，有时也并不比普通的哈希索引更有优势。

 

SPL 专门为多层序号索引提供了数据类型，称为排号键。由两个 long 型组成，long 的每个字节表示一层，所以每层序号范围是 0-255，最多可以支持 16 层序号。

例如，我们要将一个身份证号去掉校验位后转换为排号键类型，必须保证每层都在 0-255 之内。可以直接按身份证号从左到右取位，每次取两位。其中的生日年份 -1900 的值也小于 255，可以作为一层。身份证 110101201601013212 和排号键的转换关系就是图 8 所示的这样：

                                                                  图 8 身份证号和排号键转换关系

由于只有 8 层，所以排号键 k 的两个 long 型只用了一个，数值是 b01017401012001。第一个 16 进制数值 b 就对应身份证号的前两位 11，其他各两位取值也是类似的。只有年份比较特殊一点，用 2016-1900=116，转换为 16 进制就是 74。

 

这里直接按身份证号从左到右取位，对实际场景不一定是最适合的。在实际应用中，要根据已知的数据分布特征调整排号键中层次次序。

 

SPL 使用排号键类型建立多层位置索引的代码大致是这样的：

	A	B
1	func	return   k(int(left(A1,2)),int(mid(A1,3,2)),int(mid(A1,5,2)),int(mid(A1,7,4))-1900,int(mid(A1,11,2)),int(mid(A1,13,2)),int(mid(A1,15,2),int(mid(A1,17,1)))
2	=T.run(id=func(A1,id)).keys@is(ID)
3	'110101201601013212
4	=A2.find(func(A1,A3))

A1 定义了一个函数，把身份证号按照图 8 的方式转换成排号键。

A2 将表中的身份证号转成排名键再用 @s 建立索引，即构建上述的树状层次结构。

A4 利用排号键索引查找身份证号。

 

实际测试证明，在相同数据量和计算环境下，使用排号键索引后，计算速度提升了近 3 倍。对比测试详细信息参见：性能优化技巧 - 多层排号键，测试结果是这样的：

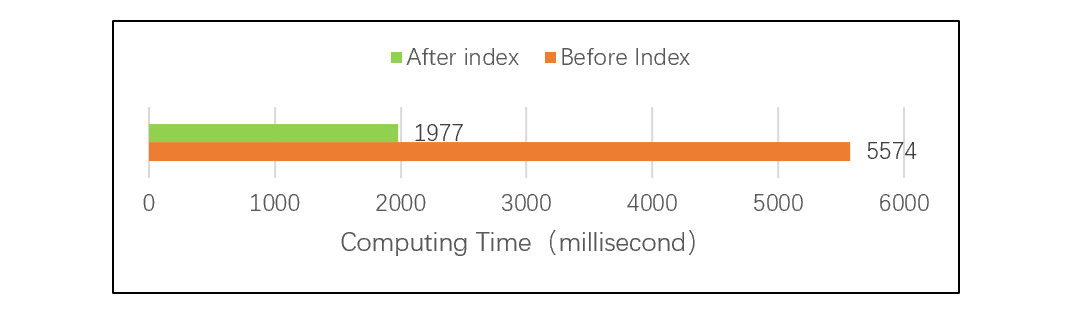
                                                                  测试结果图 2：排号键索引对比测试