Python 和 SPL 对比 9——逆分组与转置
分组后再汇总，通常会得到一个比原集合更小的集合，相当于做了聚合；逆分组相当于分组的逆运算，用一个较小的数据表通过某种规则计算出一个更大的数据表；转置也就是常说的行转列，相当于是分组的变种，逆转置又是逆分组的变种，本文对比 Python 和 SPL 逆分组与转置的运算能力。
逆分组
分组汇总后的数据一般已经失去明细信息了，不能实现逆向计算，但有时可以根据特定的规则来完成逆分组运算。如：
根据客户的贷款金额、还款期数和利率列出客户的还款明细（包括：当期还款额、当期利息、当期本金、剩余本金）。客户贷款部分信息如下：
Python
import numpy as np import pandas as pd loan_file="D:\data\loan.txt" loan_data=pd.read_csv(loan_file,sep='\t') loan_data['mrate']=loan_data['RATE']/(100*12)
loan_data['mpayment']=loan_data['AMOUNT']*loan_data['mrate']*np.power(1+loan_data['mrate'],loan_data['TERM']) /(np.power(1+loan_data['mrate'],loan_data['TERM'])-1)
loan_term_list = [] for i in range(len(loan_data)): tm=loan_data.loc[i]['TERM'] loanid=np.tile(loan_data.loc[i]['ID'],tm) loanamt=np.tile(loan_data.loc[i]['AMOUNT'],tm) term=np.tile(loan_data.loc[i]['TERM'],tm) rate=np.tile(loan_data.loc[i]['RATE'],tm) payment=np.tile(np.array(loan_data.loc[i]['mpayment']),tm) interest=np.zeros(tm) principal=np.zeros(tm) principalbalance=np.zeros(tm) loan_amt=loanamt[0] for j in range(tm): interest[j]=loan_amt*loan_data.loc[i]['mrate'] principal[j]=payment[j]-interest[j] principalbalance[j]=loan_amt-principal[j] loan_amt=principalbalance[j] loan_data_df=pd.DataFrame(np.transpose(np.array([loanid,loanamt,term,rate,payment,interest,principal,principalbalance])),columns=['loanid','loanamt','term','rate','payment','interest','principal','principalbalance']) loan_term_list.append(loan_data_df)
loan_term_pay=pd.concat(loan_term_list,ignore_index=True) print(loan_term_pay) |
月利率
月还款额
循环客户
利息 当期本金 剩余本金
创建 Dataframe
合并所有客户 |
Python的做法没啥好说的，就是按照分期贷款的计算公式（网上抄的）一步一步硬编码，最后再组合成Dataframe，没什么亮点可言。
SPL
A |
B |
|
1 |
D:\data\loan.txt |
|
2 |
=file(A1).import@t() |
|
3 |
=A2.derive(RATE/100/12:mRate,AMOUNT*mRate*power((1+mRate),TERM)/(power((1+mRate),TERM)-1):mPayment) |
/计算月利率和月还款额 |
4 |
=A3.news((t=AMOUNT,TERM);ID, AMOUNT,mPayment:payment,TERM,RATE,t*mRate:interest,payment-interest:principal,t=t-principal:principlebalance) |
/逆分组 |
SPL提供了逆分组函数news，它本质上是一个两层循环函数，先针对 A2做循环函数，再针对第一个参数term做循环函数，分号后面的参数实质上针对内层循环函数的，即这里的t是针对TERM这一层而言的，也就是第几期贷款，每期开始的需还款金额t都会变化。
列扩展成行
列扩展成行是比较常见的扩展运算，如：
现有学生成绩表如下：
将其扩展为 STUDENTID,SUBJECT,SCORE 的成绩表。
Python
score_file="D:\data\SCORES2.csv" score_data=pd.read_csv(score_file) clm=score_data.columns[1:] subject_score=score_data.melt(id_vars="STUDENTID",value_vars=clm,var_name='SUBJECT',value_name="SCORE") print(subject_score) |
需要扩展的列名 列扩展成行
|
Python利用 melt 函数完成列扩展成行的运算。
SPL
A |
B |
|
… |
… |
|
6 |
D:\data\SCORES2.csv |
|
7 |
=file(A6).import@tc() |
|
8 |
=A7.fname().m(2:) |
/需扩展的列名 |
9 |
=A7.news(A8;STUDENTID,~:SUBJECT,A7.~.field(~):SCORE) |
/列扩展成行 |
SPL 可以利用 news(…) 函数完成这一运算，写起来也不费劲，展示了列扩展成行的运算本质，相当于分组的逆运算。因为这种运算很常见，SPL 还提供了现成的函数来完成这一运算，那就是 pivot@r() 选项，代码写出来是这样的：
A9=A7.pivot@r(STUDENTID;SUBJECT,SCORE;${A8.concat@c()})
对于这种除STUDENTID外其它字段都要被扩展的情况，还可以进一步简化：
A9=A7.pivot@r(STUDENTID;SUBJECT,SCORE)
转置
和上例相反，有时还会做上例的逆运算，也就是行转成列，叫作转置。如：
现有学生成绩表如下：
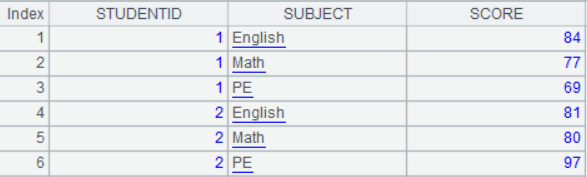
请将上表整理成以各科目为标题的成绩表。
Python
score_file1="D:\data\SCORES1.csv" score_data1=pd.read_csv(score_file1) scores=score_data1.pivot(index='STUDENTID',columns='SUBJECT',values='SCORE') print(scores) |
转置
|
Python利用 pivot(…) 函数完成转置运算，pivot 和 melt 函数相当于是逆运算。
SPL
A |
B |
|
… |
… |
|
11 |
D:\data\SCORES1.csv |
|
12 |
=file(A11).import@tc() |
|
13 |
=A12.pivot(STUDENTID;SUBJECT,SCORE) |
/转置 |
SPL 有 pivot 函数，轻松完成转置运算，pivot 函数的 @r 选项就是它的逆运算，上例已经介绍过。转置运算是分组运算的变种，来看下 SPL 用分组的方式如何完成转置：
A13=A12.group(STUDENTID;${A12.id(SUBJECT).("~.select@1(SUBJECT==\""+~+"\").SCORE:"+~).concat@c()})
这里的宏较复杂，但仔细研究也能看明白，也就是将当前分组子集中与某个学科名称相同的分数取出来作为分组后序表该学科字段的取值。这么写只是说明，转置运算是分组的变种，实际中只要用 pivot 来做就可以了。
小结
Python 没有提供逆分组函数，整个逆分组过程都是硬编码，没有什么技巧可言；melt 与 pivot 函数互为逆运算，行列转换还是比较方便的。
SPL 的 news 函数使得逆分组过程简单，完成复杂的逆分组运算也只要 1 行代码；pivot 函数结合 @r 选项完成行列转换运算。通过本文介绍，进一步理解行列转换与分组之间的关系了，还可以发现即使使用分组函数 group 或者逆分组函数 news 完成行列转换也没那么难。
对润乾产品感兴趣的小伙伴，一定要知道软件还能这样卖哟性价比还不过瘾？ 欢迎加入好多乾计划。
这里可以低价购买软件产品，让已经亲民的价格更加便宜！
这里可以销售产品获取佣金，赚满钱包成为土豪不再是梦！
这里还可以推荐分享抢红包，每次都是好几块钱的巨款哟！
来吧，现在就加入，拿起手机扫码，开始乾包之旅
嗯，还不太了解好多乾？
英文版