拟合曲线趋势
算法背景
很多仪表设备都能定时产生一些数据,称之为时间序列。
下图是一张时间序列的走势图,横轴是时间(dd hh:mm),纵轴是数值。
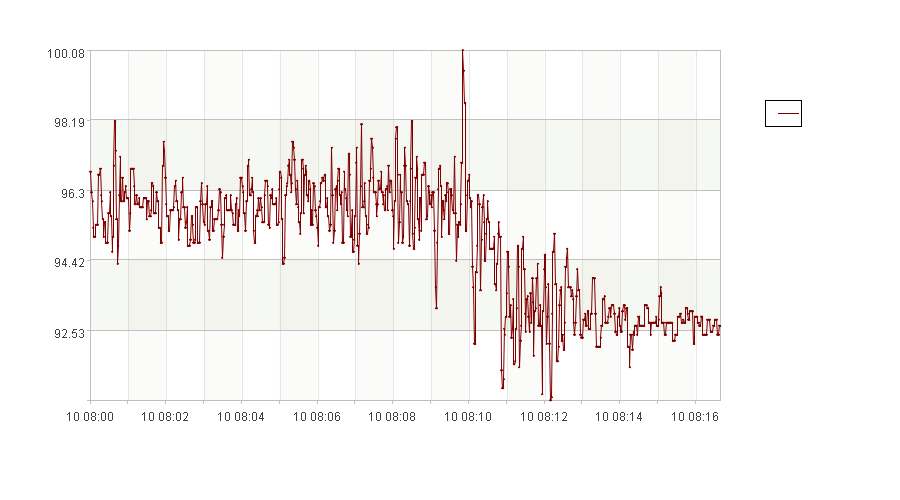
数据的波动很大,看局部会有点杂乱无章的感觉,但观察整张图又隐约可以看出曲线的走势(平稳——下降——平稳),能不能用数学方法把曲线的总体走势描述出来呢?这样将有利于分析设备仪表的工作状况。
答案是可以的。
下面就来介绍如何利用原始数据拟合出曲线的趋势线。
算法原理
我们把描述时间序列趋势的曲线称为主线。主线上相邻点之间的距离称为主线距离,同一时刻主线上的点与原值的距离称为原值距离。我们当然希望主线是平滑的,否则就和原值一样看起来杂乱无章了,所以所有的主线距离之和要尽量小,也就是说主线相邻点的值变化小,这样主线就会少一些剧变,更平滑一些。同时主线要能表征原值的特点,所以也要与原值接近,否则只考虑平滑时主线就成一条平直线了,这时候就要求所有的原值距离之和也要尽量小,这样主线偏离原值就更少。以这两者加权后的总和最小为目标,就可以拟合出一条主线,而调整权重则可以使主线更平滑或者更接近原值。
算法过程
时间序列用X表示:
X=[x1,x2,…,xn]
其中xi是序列X的第i个元素。
设主线为M:
M=[m1,m2,…,mn]
其中mi是序列M的第i个元素。
1. 计算主线距离
主线距离用MD表示
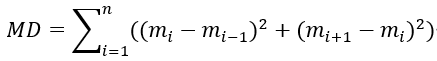
原值距离用VD表示。
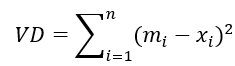
2. 平衡两类距离的最小值
设置平衡系数k来平衡两类距离的权重,则总距离D
D=VD+k*MD
3. 优化mi使总距离D最短
对每个mi求偏导:
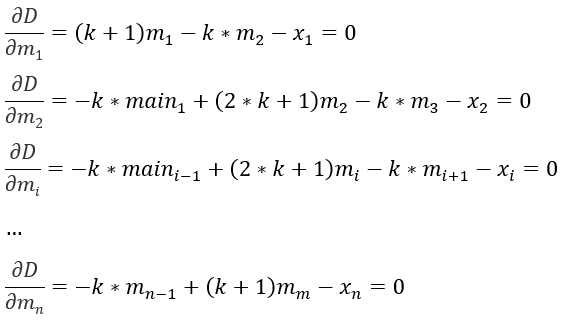
转换后的问题变为解多元线性方程问题。
系数矩阵用C表示
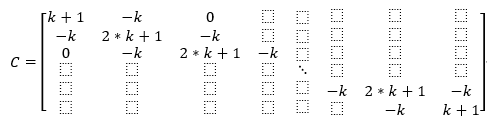
矩阵中未填写数值处都是0。
C*M=X
解上述方程就得到了主线M。
M=linefit(C,X)
其中linefit()是解线性方程的函数。
这里需要说明两点:
1. 平衡系数调节两类距离的权重,k越大,主线距离MD占比越大,主线越平滑,k越小,原值距离VD占比越大,主线越接近原值。当k=0时,主线就是原值。当k=∞时,主线是一个常数,常数值等于原值的平均值。
2. 系数矩阵C是一个n*n方阵,因此它的计算受到了这个方阵大小的限制(n很大时,计算机内存很可能存不下这个n*n方阵)。仔细观察系数矩阵C,可以将其转换一个n*3的矩阵,利用矩阵变换规则同样可以求得主线M,这样就可以求n很大时的主线。
写出代码
A |
B |
C |
D |
E |
|
1 |
=seq |
/输入参数:时间序列 X |
|||
2 |
=k |
/平衡系数:k |
|||
3 |
=func(A6,A1,A2) |
/拟合主线 |
|||
4 |
return A3 |
||||
5 |
/拟合主线 2,参数:时间序列 X,参数 k |
||||
6 |
func |
||||
7 |
1e15 |
||||
8 |
=if(B6==0,A6,if(B6>=B7,((avg=round(A6.avg(),6),A6.(avg))),func(A11,A6,B6))) |
||||
9 |
return B8 |
/k=0时,主线=原值。k=∞时,主线=常数=原值的平均值。 |
|||
10 |
/拟合主线(相邻两数之差的平方和 + 原值与该数的差的平方和最小),参数:序列,参数 k |
||||
11 |
func |
||||
12 |
=transpose(A11) |
/x |
|||
13 |
=B12.len() |
||||
14 |
=B13.(if(#==1,[B11+1,-B11,0],if(#==B13,[0,-B11,B11+1],[-B11,2*B11+1,-B11]))) |
/系数矩阵 C |
|||
15 |
=func(A18,B14,B12) |
/矩阵变换 |
|||
16 |
=func(A37,B15(1),B15(2)) |
/解方程 |
|||
17 |
/矩阵变换,参数:系数矩阵 C,原值 X |
||||
18 |
func |
||||
19 |
for A18.len() |
1e-7 |
|||
20 |
if B19==1 |
=A18(B19).select@1(abs(~)>C19) |
/除数 |
||
21 |
else if B19==A18.len() |
||||
22 |
=A18(B19).m(2) |
||||
23 |
=A18(B19)=A18(B19)++A18(B19-1).(~*(-D22)) |
/更新 c=c+c[-1] |
|||
24 |
=B18(B19)=B18(B19)++B18(B19-1).(~*(-D22)) |
/更新 x=x+c[-1] |
|||
25 |
=D20=D23.m(-1) |
/除数 |
|||
26 |
else |
=A18(B19-1).pselect@a(abs(~)>C19) |
/错位 |
||
27 |
=A18(B19).~ |
||||
28 |
=A18(B19)(to(2))=A18(B19)(to(2))++A18(B19-1)(D26).(~*(-D27)) |
/更新 c=c+c[-1] |
|||
29 |
=B18(B19)=B18(B19)++B18(B19-1).(~*(-D27)) |
/更新 x=x+c[-1] |
|||
30 |
=D20=D28.m(-1) |
/除数 |
|||
31 |
=A18(B19).(~/D20) |
/c除以除数 |
|||
32 |
=A18(B19)=C31 |
/更新 c |
|||
33 |
=B18(B19).(~/D20) |
/x除以除数 |
|||
34 |
=B18(B19)=C33 |
/更新 x |
|||
35 |
return [A18,B18] |
||||
36 |
/解方程,参数:系数矩阵 C,X |
||||
37 |
func |
||||
38 |
=A37.(if(#==1,~.m(:2),~.m(2:))) |
/第一行是前两个元素,其他是后两个元素 |
|||
39 |
=B38.rvs() |
/c倒序 |
|||
40 |
=B37.rvs().conj() |
/x倒序 |
|||
41 |
=B40.iterate@a(if(#==1,~~,~-(B39(#).m(-1)*~~)),B40.~) |
/迭代更新 c |
|||
42 |
=B41.rvs().(round(~,6)) |
/恢复原序 |
|||
输入参数说明:
1. seq:时间序列X
2. k:平衡系数k,k越大,主线越平滑。
3. 代码是用矩阵变化的方式解方程的,因此n可以很大。
应用举例
时间序列X如下图:

图中横轴是时间(dd hh:mm),纵轴是序列中的值。
不同k的主线如下图:
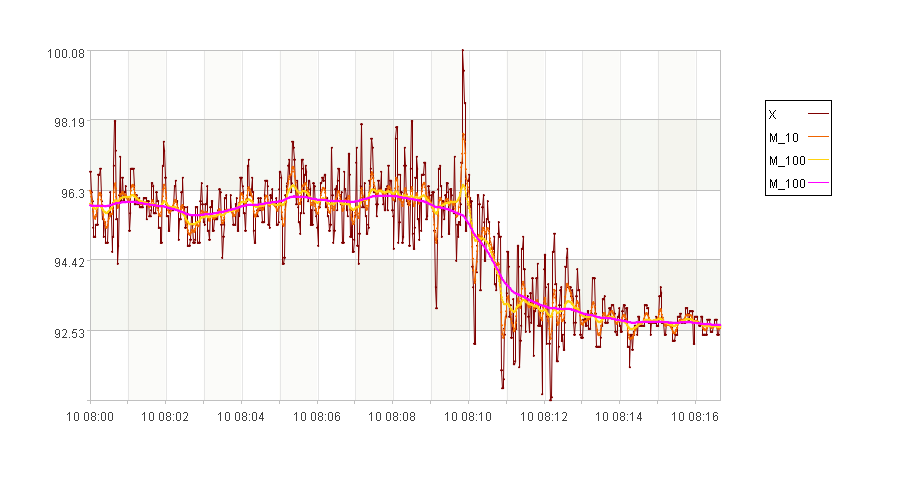
M_10:k=10时的主线。
M_100:k=100时的主线。
M_1000:k=1000时的主线。
k越大时,主线越平滑。



