【程序设计】10.4 [找关联] 连接
10.4 连接
接着上面这个订单例子,我们希望把两份文件中订单号相同但内容不同的记录挑出来之后。将字段(订单号除外)都拼到一起对照着看。也就是要想形成一个两倍字段数(除订单号)的数据表。
我们通常使用 join 函数来完成这个任务。
A |
B |
|
1 |
=T("data1.xlsx") |
=T("data2.xlsx") |
2 |
=[A1,B1].merge@i(ID) |
=[B1,A1].merge@i(ID) |
3 |
=join(A2:a,ID;B2:b,ID) |
|
4 |
=A3.new(a.ID:ID,a.Company:CompanyA,b.Company:CompanyB, a.Area:AreaA,b.Area:AreaB,a.OrderDate:OrderDateA,b.OrderDate:OrderDateB, a.Amount:AmountA,b.Amount:AmountB, a.Phone:PhoneA, b.Phone:PhoneB) |
|
A3 的 join 函数返回一个有两个字段的序表,分别为 a 和 b,它会将 A2 和 B2 中的记录按 ID 字段值拼起来,也就是把 ID 相同的 A2 记录和 B2 记录分别填入 a 和 b 字段,作为返回序表的一条记录。字段 a,b 的取值也是记录,这有点像外键被 switch 转换后的结果。搞清了 A3 的运算结果, A4 写起来虽然长,但却很容易理解了。
和 merge 不同,join 的任务常常是把数据表变得更宽,而 merge@u 则会把数据表变长 (记录数更多)。
和 merge 更大的不同在于,merge 针对的数据表一般是相同数据结构的。而 join 更常用的场景是两个(也可以更多)数据结构不同的数据表。
还是前面生成的人员表例子,我们现在有一份有性别、身高、体重的人员表,还有一份有国籍、部门的员工表。我们想把这两个表拼成一个更宽的表,假定人员表的 name 字段和员工表的 eid 字段相同时就表示是同一个人。
整理一下数据生成的代码,部门表暂时没有用,先不要了。
A |
B |
C |
|
1 |
=100.sort(rand()) |
[HR,R&D,Sales,Marketing,Admin] |
[CHN,USA] |
2 |
=100.new(A1(#):eid,C1(rand(2)+1):nation,B1(rand(5)+1):dept) |
||
3 |
=100.new(string(~):name,if(rand()<0.5,"Male","Female"):sex,50+rand(50):weight,1.5+rand(40)/100:height) |
||
员工表 A2 中 eid 的次序中乱的。
我们来完成所说的任务:
A |
B |
C |
|
… |
… |
||
4 |
=join(A3:P,int(name);A2:E,eid) |
||
5 |
=A4.new(P.name,P.sex,P.weight,P.height,E.nation,E.dept) |
||
因为 A3 的 name 是字符串类型,和 A2 的 eid 不同,所以要做个转换,写成 int(name)。也可以转换 A2,把 A4 写成:=join(A3:P,name;A2:E,string(eid))。
A4 的运算结果是这样的:
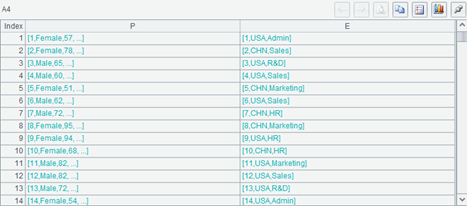
一个有两个字段的序表,字段取值分别是 A3 和 A2 的记录。因为我们没有为 A2 和 A3 设置主键,开发环境会把记录的字段显示成序列的样子。可以看出来,同一行左边两边的记录的第一个字段, 也就是 name 和 eid,都是相同的。这就是 join 运算的结果,它会把 A3 的 name 和 A2 中 eid 相同的记录拼到一起(其实是 int(name) 和 eid 相同,但看起来是一样的)。
然后 A5 就很容易得到期望的结果了,不再详细解释了。
两个数据表可以通过某个字段(或表达式)相等的关系生成了一个有两个字段数据表,再基于这个新数据表就可以同时引用两个原来数据表的字段进行运算,这样就完成了两表的关联。用于判定关联的字段(表达式)称为关联键,关联键值相等记录互称为关联记录。这种关联运算称为连接。
前面节中讲过的外键关联也是一种连接运算,它是以事实表的外键和维表的主键作为关联键的。不过,我们很少把外键关联的运算结果表示成以两个取值为记录的字段为数据结构的序表,而是习惯于用前面的办法,用 switch 转换外键,或用 join(不是现在这个 join)把维表字段拼接到事实表上。
如果我们为 A2 和 A3 这两个表设置了主键,那么再 join 时就可以不写这个关联键了。
A |
B |
C |
|
1 |
=100.sort(rand()) |
[HR,R&D,Sales,Marketing,Admin] |
[CHN,USA] |
2 |
=100.new(A1(#):eid,C1(rand(2)+1):nation,B1(rand(5)+1):dept).keys(eid) |
||
3 |
=100.new(~:name,if(rand()<0.5,"Male","Female"):sex,50+rand(50):weight,1.5+rand(40)/100:height).keys(name) |
||
4 |
=join(A3:P;A2:E) |
||
这时候要改一下 A3 的生成语句,直接用整数作为 name 字段的值,这样两个表的主键不需要转换而直接作为关联键。
使用主键作为关联键的连接称为同维关联,这两个表也互称为同维表。数据库的术语中,同维关联是一种一比一的关联,也就是某个关联表中的一条记录只会和另一个关联表中的一条记录关联,不会多条,因为主键是唯一的。
我们继续这一段代码,把前几行数据生成的代码改一下,A2 在 1-100 之间随机选 80 个整整数作为主键,生成 80 条记录; A3 则直接选 1-90 作为主键,生成 90 条记录。这样,A2 和 A3 的主键仍会有不少共同的,但也各自会有少量主键值是对方没有的。(因为随机生成,每次运行的结果可能不同,但不影响我们讨论问题)
A |
B |
C |
|
1 |
=100.sort(rand()) |
[HR,R&D,Sales,Marketing,Admin] |
[CHN,USA] |
2 |
=80.new(A1(#):eid,C1(rand(2)+1):nation,B1(rand(5)+1):dept).keys(eid) |
||
3 |
=90.new(~:name,if(rand()<0.5,"Male","Female"):sex,50+rand(50):weight,1.5+rand(40)/100:height).keys(name) |
||
4 |
=join(A3:P;A2:E) |
||
5 |
=A4.len() |
=A2.(eid)^A3.(name) |
=B5.len() |
再看 A4 的结果:
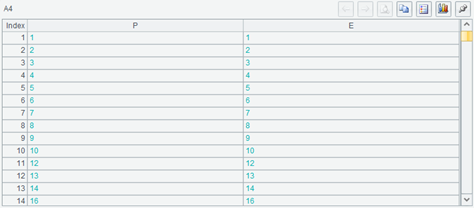
仍然是左右都相等,但明显有缺失的序号(也就是主键)。
而看 A5,它当然不会是 100,但也即不是 80 也不是 90,而是更小。
join 函数会找出两个表的关联键都存在且相等的记录来关联,如果有一方的关联键值在另一方不存在,则这一方的相应记录也会被舍弃。这种连接方式称为内连接。它计算出来的结果序表中还有的关联键集合,是两个参与关联的序表的关联键集合的交集,即上面代码中的 B5,而 A5 也必然会与 C5 相等,通常会小于 A2 或 A3 的长度。
我们改动后两行代码再尝试:
A |
B |
C |
|
… |
… |
||
4 |
=join@1(A3:P;A2:E) |
||
5 |
=A4.len() |
=A3.(name) |
=B5.len() |
再执行,看 A4
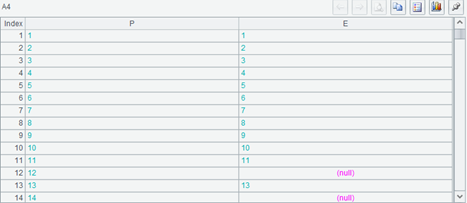
P 字段取值中的记录主键是完整的,从 1 排到 90,和 A3 的记录一一对应。有个别记录 E 字段填成了 null。A5 也是 90,和 A3 长度相同。
有 @1 的 join 将会以左边的关联表(第一个参数)为基准,右边关联表中如果有与左边关联键相同的记录,则关联上,如果没有,则会填成空。结果序表的关联键值和和左边关联表一值,其长度也和左边关联表相同。
这种以左边为准的连接方式称为左连接。
有些数据库体系还有右连接,也就是以右边为准。不过 SPL 没有提供了,因为只要把参数换个位置就可以了,没有太大的必要。
而且这个 @1 是数字 1 不是字母 l,它表示以第 1 个为准。
继续:
A |
B |
C |
|
… |
… |
||
4 |
=join@f(A3:P;A2:E) |
||
5 |
=A4.len() |
=A2.(eid)&A3.(name) |
=B5.len() |
再看 A4:
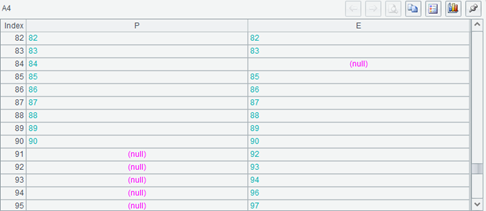
因为 A3 的主键是从 1-90,前面的记录存在,要把表格拉到后面一点,从最后几条记录就可以看出来了。
现在左右两边都有 null 的字段值了,A5 也大于 90 了,但也经常不是 100。
有 @f 的 join 将会两边都兼顾,关联键值在任何一方存在,就会在结果序表中生成一条记录,如果双方都存在有关联键值的记录,则将记录填入相应的字段实现关联。如果某个关联键值只有一方有对应的记录,则填入相应的字段,并将另一方面相应的字段值填空。最后结果序表中还有的关联键值集合,将是两个参与关联的序表的关联键集合的并集,还是代码中的 B5,而 A5 也会和 C5 相同,通常会大于 A2 或 A3 的长度。
这种两边兼顾的连接方式称为全连接。
内连接,左连接和全连接是非常重要的概念,在执行连接运算时一定要搞清要采取那种连接,不同方式的连接结果会很不一样。
外键关联通常是左连接,即以事实表为准,switch 函数如果找不到维表中的关联记录则会把外键字段填空。而 switch@i 则相当于内连接,找不到关联记录时会把事实表的相关记录也过滤掉。
join 和 join@f 还有点类似 merge@i 和 merge@u,事实上也确实可以用连接运算来实现两个序表针对主键交和并的运算。
一份数据可能有多个制作来源,然后再拼接成完整的数据。有可能是按行(记录)分成多个部分,那将用 merge 来合并,过程中要处理重复的部分。也可能是按列(字段)分成多个部分,这时候用 join 来合并,也需要把这些数据合理地拼接,不能错位。
再来看另一种关联情况:
A |
B |
C |
|
1 |
=100.sort(rand()) |
[HR,R&D,Sales,Marketing,Admin] |
[CHN,USA] |
2 |
=100.new(A1(#):eid,C1(rand(2)+1):nation,B1(rand(5)+1):dept).keys(eid) |
||
3 |
=A2.news(12;eid,~:m,5000+rand(5000):salary).keys(eid,m) |
||
在员工表的基础上为每个人生成了 12 个月的工资表,A3 需要两个字段来做主键了(才能保证唯一)。
现在我们想计算每个部门的总收入。
部门信息在员工表中,而收入信息中工资表中,这需要做两个表的关联。
用我们学过的外键关联,把员工表看成是工资表的维表,这样就可以解决了:
A |
B |
C |
|
… |
… |
||
4 |
=A3.switch(eid,A2) |
=A4.groups(eid.dept;sum(salary)) |
|
这个代码没有问题。不过,这种用主键的一部分作为外键的关联关系,我们还会使用 join 来处理。
A |
B |
C |
|
… |
… |
||
4 |
=join(A2:E;A3:S,eid) |
=A4.groups(E.dept;sum(S.salary)) |
|
和刚才计算出同样的正确结果。
看看 A4,它算出来的结果是这样:
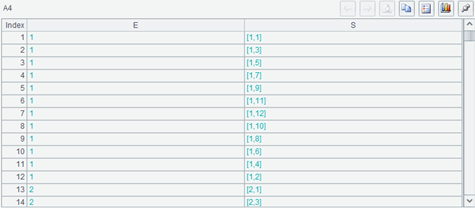
A2 的记录在 E 字段中重复了,每一条 A3 的记录都关联了一条 A2 的记录,而每一条 A2 的记录则关联了 12 条 A3 的记录,最后 A4 的长度和 A3 相同。
这种用一部分主键字段作为外键的关联,又称为主子关联。主键字段较少的表称为主表,较多的则称为子表。主子关联是一种一对多的关联,和外键关联正好相反。站在子表的立场上看主表就是外键关系,而站在主表立场上看子表则是主子关联。
主子关联时我们也会使用这种 join 来处理,而不总是使用 switch 和前面节讲过的 join。有时也会把子表先做 groups 后再与主表 join,比如刚才的问题:
A |
B |
C |
|
… |
… |
||
4 |
=A3.groups(eid;sum(salary):salary).keys(eid) |
||
5 |
=join(A2:E;A4:S) |
=A5.groups(E.dept;sum(S.salary)) |
|
A4 执行分组汇总后形成了以分组键为主键的序表,和 A2 就是一对一的同维关联了。
理论上,外键关联时,我们也可以把事实表以外键作为分组键做 groups 形成可以和维表进行同维关联的表,但通常不会这么做,因为一个事实表经常会有多个外键,按某个外键做了 groups,其它外键就没法处理了。而子表在绝大多数情况下只会有一个主表,所以针对关联键去做 groups 再与主表做同维关联是没什么问题的。
当然,外键关联时也可以像主子关联时直接用 join 函数来执行连接运算,把维表和事实表记录拼起来,一条维表记录可能关联多条事实表记录。其实,外键那一节中讲的 join 函数就是在这么做,只不过同时把关联后引用维表的字段动作一起做了,因为这种组合动作更为常见,结果序表长度也是和事实表(主子关联概念中的子表)长度相同,所以那个函数也被命名为 join。
我们现在碰到过一对一、一对多、多对一这几种连接方式,那么还有没有多对多的情况?
结构化数据运算中几乎不存在有业务意义的多对多连接,多对多连接只存在于理论分析或数学运算中,日常数据处理中基本上不会碰到与主键无关的关联,可以不必关注。
SPL 提供了 xjoin 函数用于处理任意条件的连接,也可以实现多对多。但我们也只能举一个数学例题来说明它。
xjoin 将计算出参与关联的集合(注意我们说集合,不再说序表了,因为结构化数据太难找出业务合理的例子)的笛卡尔集,过程可对这个笛卡尔积作指定条件的过滤。
笛卡尔集的概念,不熟悉的读者可以上网搜索,我们简单举个例子来理解。
A |
B |
C |
|
1 |
[1,2,3] |
[HR,R&D,Sales,Marketing,Admin] |
[CHN,USA] |
2 |
=xjoin(A1:a;B1:b) |
=xjoin(A1:a;B1:b;C1:c) |
=xjoin(A1:a;C1:c) |
观察 A2、B2、C2 的计算结果,并不是很难看明白。在每个集合中各取一个成员构成一条记录,所有可能的组合都穷尽了,就是笛卡尔积。也可以理解成多层循环,每层针对一个集合循环,最内层循环中把每层的循环变量收集起来构成一条记录,这些记录的集合就是结果序表,其长度是参与计算的几个集合长度的乘积。
事实上,我们之前说过的所有关联都可以定义成这样:参与关联的数据表的笛卡尔积中取一个满足某个条件的子集(我们学过的连接运算都可以用“关联键值相等”这样的条件),SQL 就是这么定义连接运算的。这个定义很简单,但是没有体现出数据之间的关联特征,对于简化语法和提高性能都没什么帮助。
SPL 没有采用这种的定义,而把常用的关联方式分别描述,读者可以在不同的场景下使用不同的运算方式。
我们来用 xjoin 实现以前用递归程序实现的排列(这里指数学上的排列)生成:
A |
B |
|
1 |
5 |
3 |
2 |
=to(A1) |
=B1.("A2:_"/~).concat(";") |
3 |
=xjoin(${B2}).(~.array()).select(~.id().len()==~.len()) |
|
A3 将计算出 1,2,3,4,5 构成的所有 3 个成员的排列。
xjoin 先计算出 3 个 to(5) 的笛卡尔积,然后过滤掉其中有重复成员的(id.len!=len),那就是一个合理的排列。可以改变 A1 和 B1 获得它数值情况的排列。
这个代码比递归看起来要简单很多,但运算量却要巨大得多,只能在较小的数值下尝试。
我们用了三章篇幅讲述了结构化数据及其运算,这些内容已经远远超过 SQL 也就是关系数据库的查询计算能力,主要运算中仅递归关联因难度较大且应用较少而被舍弃了。
也就是说,学完了这些内容并能够灵活组合运用,已经比只会用 SQL 的专业数据库程序员对结构化数据的驾驭能力更强了。再配合 Excel 等表格软件来实现美观的呈现,就能够轻松解决日常数据处理的几乎所有问题。



