5.2 循环函数

前面我们用循环语句完成针对序列成员的求和、最大 / 最小值运算，但循环语句很麻烦，要先设置初始值再一步步计算。SPL 考虑到这一点，提供了一些针对序列的常用函数。

很容易从这些函数的名称中看出其意义，再执行这段代码观察运算结果以确认。count()和 len() 有点像，但 count()不统计值为 null 的成员。avg() 定义为 sum()/count()，注意不是 sum()/len()。

我们会通俗地这种把序列计算成一个单值的函数称为聚合函数，相当于对集合做了聚合。

这些聚合函数都使用了 x.f() 这种对象式的语法。其实，SPL 也支持把这些函数写成传统形式，而序列成员作为参数：

我们之前已经用过 max/min 函数了。

需要指出的是，len()不被认为是聚合函数，它实际上是取出序列的一个属性，并没有实际遍历序列成员计算出结果，所以 len() 也没有这种把序列成员写成参数的写法。

我们知道，用 to(n)能够产生序列 [1,2,…,n]，再用 sum()函数求和，这样我们可以轻易地用 to(100).sum()计算出 1+2+…+100 了，比之前用循环语句的代码简单了很多。

那么，进一步，想计算前 100 个奇数之和呢？似乎还得写循环语句？

不，SPL 已经想到了这个问题，并提供了方法从已有序列生成一个同样长度的新序列。这样一句表达式 to(100).(~*2-1).sum() 就可以计算出前 100 个奇数之和了。

左边的 to(100) 和右边的.sum()我们能理解了，但中间的.(~*2-1) 是个什么东西？

对于序列 A，A.(x) 表示针对 A 的每个成员计算表达式 x，并将这些计算结果再按同样次序构成的同样长度的序列。而在 x 中用符号 ~ 来表示正在参与计算的那个 A 的成员。

[1,2,3].(~*2-1) 就是 [1*2-1,2*2-1,3*2-1] , 也就是 [1,3,5]，把 ~ 依次替换成每个序列成员就可以了，它实际上就是循环序列时的循环变量。

这样我们就能理解 to(100).(~*2-1).sum()了，类似地，to(11,20).(~*~).sum() 可以计算从 11 到 20 这 10 个数的平方和。

A.(x).sum()这种写法很常见，SPL 中可以简化写成 A.sum(x) 的形式，这样即简单又更容易理解。进一步，to(n) 上的函数也常用，SPL 允许它简化写成 n.f(…) 的样子。

1+2+…+100 就可以写成 100.sum()，而前 100 个奇数和也可以写成 100.sum(~*2-1)。是不是非常简单。

针对序列每个成员计算，遍历后得到出一个新结果的函数，我们通称为循环函数。A.(x) 和聚合函数以及简化形式的 A.f(…) 都是循环函数。

欧拉发现过一个与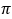相关的公式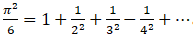：。我们用它反过来计算 ，只要一个表达式：=sqrt(1000.sum(1/~/~)*6)，计算前 1000 项，精度足够了。

与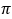相关的公式很多，这里还有一个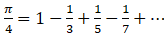：。在 if 函数的配合下，也很容易实现出来：=1000.sum(if(~%2==1,1,-1)/(2*~-1))*4。

循环函数的语法非常简洁高效。

我们再来简化学习循环时使用的例子，计算。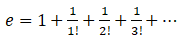

之前用循环语句实现时，我们使用了中间变量来计算 n!，但在 ~ 中似乎写不出来了？

其实在表达式中也可以使用中间变量，改写出不用循环语句的代码是这样：

这个 sum 内的表达式中使用了逗号运算符，即 (a,b,c,…,x) 将依次计算 a,b,c,…,x，最后返回的计算结果为 x。(nf*=~,1/nf)就会计算 nf*=~（回忆一下 = 可以作为运算符），再计算 1/nf，最后的计算结果是 1/nf。逗号运算符也是 C 语言发明并被 SPL 继承下来的，使用它可以将一些少量多步的运算写在一个表达式中，避免写成多个语句。逗号运算符的表达式通常要写到一个括号里，以确保不会错误识别，比如这里，如果不写外层的括号，有可能会被 sum 函数认为是多个参数而加起来，这就得到错误的结果了。

现学现卖，还可以用逗号运算符把两格代码并成一格：

对于斐波那契数列，我们有了序列这个武器后，可以把数列的前 n 项都算出来：

A2 将计算出斐波那契数列的前 20 项，这里的表达式没有用到充当循环变量的 ~，循环函数仅用来实现重复的计算。

这个代码看起来有点难懂，其原理和之前讲循环语句时的例子代码是一样的，我们不再细说，请读者自行思考，在纸上画一画手工执行一遍就能理解了。

【程序设计】 前言及目录
【程序设计】5.1 [一把抓] 集合运算
【程序设计】5.3 [一把抓] 循环函数进阶