八皇后
八皇后问题是一个古老而著名的问题。具体为:在 8X8 格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,请问有多少种摆法。
A |
B |
C |
D |
|
1 |
8 |
=[0]*A1 |
>i=1 |
|
2 |
for i>0 |
>B1(i)+=1 |
||
3 |
if B1(i)>A1 |
>B1(i)=0,i-=1 |
next |
|
4 |
if i==1 && A1>1 |
>i=2 |
next |
|
5 |
=B1(i) |
=B1.to(i-1) |
||
6 |
if C5.pselect(~==B5|| i-# ==abs(B5-~)) |
next |
||
7 |
if (i+=1)>A1 |
=@|B1.concat@c() |
>i-=1 |
|
8 |
=C7.len() |
https://try.esproc.com/splx?3NH
将N*N格的国际象棋上的每一行作为一个序列,将列上的每一个格子按顺序编号 1,2,3,…,N,皇后必须放在不同的行中,每行1个。A1定义准备放置的皇后个数N, A2初始化每行皇后的位置为0。C1定义当前判断的行号i,从第1行开始。
A2开始执行循环,当行号i不大于0时说明循环结束,结束循环。B2将当前行的皇后顺移1位。B3判断,如果本行皇后的列位置大于N,说明本行所有位置均完成尝试,将本行皇后移除,并返回上一行继续调整皇后位置。第4行,对于仅有1行的情况,无需判断是否合理,直接继续去设置第2行的皇后,如果N为1则直接执行后续判断。
A5取出当前皇后位置,C5取出前面各行的皇后位置。
B6判断,如果皇后和已有的某个棋子在同一列或者在同一斜线上,说明不合理,继续判断下个位置。
如果当前皇后的位置和已有的棋子不冲突,则在B7递增行号i,并判断是否所有皇后都已经正确放置。如果成功,则各个皇后的位置记录在C7中,并继续检测本行是否还有其它位置可行;否则开始放置下个皇后。SPL中,用A.concat@c(),可以将序列中的成员用逗号分隔连接为字串。
循环完毕后,可以在C7中看到所有可能的解法:
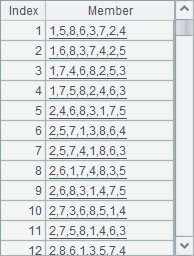
C7序列的成员总数就是摆法的种数,如果无解则C7和A8中都将得到空值:

也可以递归调用子程序递归执行,尝试放置下一行的皇后:
A |
B |
C |
D |
|
1 |
8 |
[] |
>queen([0]*A1,1) |
=B1.len() |
2 |
||||
3 |
func queen(a,r) |
if r>A1 |
>B1|=a.concat@c() |
return |
4 |
for A1 |
if r>1 && a.to(r-1).pselect(~==B4 || r-#==abs(B4-~)) |
next |
|
5 |
>a(r)=B4 |
>queen(a,r+1) |
https://try.esproc.com/splx?3VU
A3定义了子程序queen(a,r),序列a记录各个皇后的位置,r为当前放置皇后的行。B3判断是否全部皇后已放置正确,成立时在B1中记录当前解,并返回。B4循环行中的每一列,C4执行判断,如果与前面各行已经摆放的皇后出现在同一列或同一斜行,说明当前位置不正确,继续尝试下一个位置。如果当前皇后位置安全,则在a中记录该位置,并继续放置下一行的皇后。
C1中调用子程序,从初始状态的第1行开始放置皇后,执行后,即可在B1中获得摆放结果,在D1中可得到共有多少种解法。
在SPL中,子程序可以递归调用,这种方式的代码更加简洁易读。




英文版