SPL 提速天体聚类任务 2000 倍
问题描述
国家天文台有个聚类任务:共 11 份数据,每份数据是从一张照片中提取出来的,包含 500 多万条记录,每条记录是一个天体的坐标及属性。11 张“照片”中有些天体坐标是重复的,但这些重复的坐标不完全相同,他们会有一些差别但距离不会太远。任务就是把其中一张“照片”作为基础,从其他照片中找出重复的天体,把重复天体的坐标及属性均值作为该天体的最终坐标和属性,即把距离很近的天体聚成一类再做聚合运算,这样就可以得到一张坐标清晰且信息更加准确的天体“照片”。
问题分析
这个任务不算复杂,只要循环基础照片中的每一个天体坐标,将其与其他照片中的每个天体坐标计算距离,不超过某个阈值就认为是同一个天体,视作一类,最后将每一类中所有天体坐标求均值就得到了该天体的坐标。
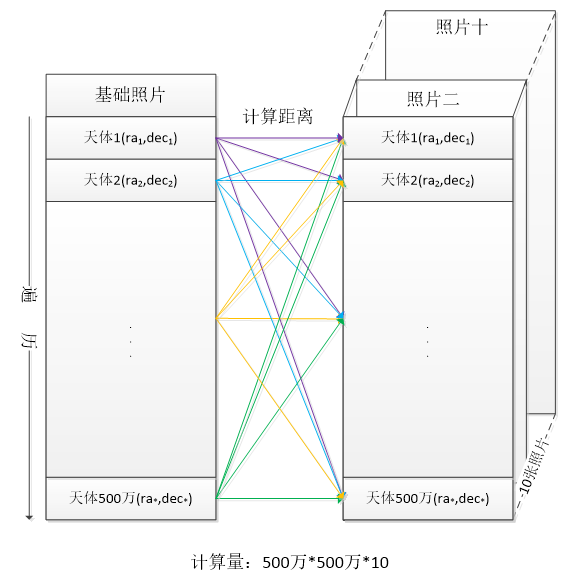
但是当用计算机计算时就发现这个任务的计算量是惊人的,基础照片需要循环 500 多万次,其中的每个天体坐标又要与其他照片中的 5000 多万个坐标计算距离,计算复杂度是 500 多万 *5000 多万,这将是个天文数字。
事实也确实如此,在实验阶段,把每张照片的数据量减小 10 倍,即每张照片的天体坐标量为 50 万,用 Python 写出代码实现上述方法计算出 11 张照片的聚类结果需要的时间是 6.5 天。按计算复杂度来算,500 多万的数据量,计算量是 50 万数据量的 100 倍,即需要耗时 650 天,这肯定是一个无法接受的数字。
同样的 50 万数据量,被装入了某分布式数据库后用 SQL 实现,动用了 100 颗 CPU 后,跑了 3.8 小时完成了计算。看起来比 Python 快了很多倍,但 Python 的 6.5 天是单线程,细算下来 SQL 的单核性能还不如 Python(3.8 小时 *100>6.5 天)。巨大的资源消耗已经难以容忍,而且计算 500 多万规模时也要 380 小时。
解决方案
我们来考虑哪里可以优化以减少计算量。
基础照片中的天体坐标是必须循环的,这样才能保证每个天体都被用来聚类了,其他照片中的天体坐标不用每次都遍历,只要找到基础天体坐标附近的坐标就可以了。这类查找任务很适合二分法,它可以大量减少计算量。
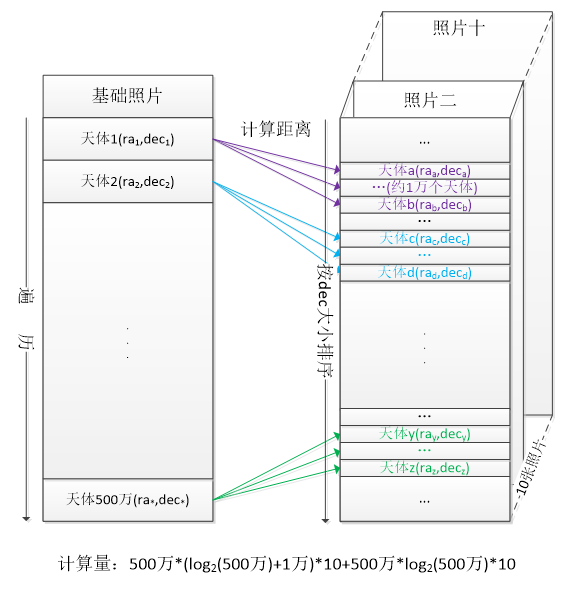
具体过程是这样的:先对每张照片中的天体坐标排序,用二分法找到某个阈值范围内的天体坐标,这样就排除了大多数天体,这是粗筛过程;用基础天体与粗筛结果中的天体计算距离,找出符合条件的结果,这是细筛过程。
来看看粗筛加细筛方法的计算量,10 张照片每张排序一次,计算量是 500 万 *log(500 万)*10;二分法粗筛,计算量是 500 万 *log(500 万)*10;细筛过程,计算量不确定,但根据经验,粗筛后的结果通常不超过 1 万个,粗筛的计算量中 log(500 万) 还要再加 1 万;这样算下来,总的计算量大概是 500 万 *log(500 万)*10+500 万 *(log(500 万)+1 万 )*10,相较于原来的方法,计算量只有原来的五百分之一。
技术选型
方法有了,还要选择程序工具,之前实现时使用 Python,不可否认 Python 很强大,有天文学计算的现成框架,比如计算距离的方法,只要调用现成的类库就可以轻松算出来。
但 Python 也有着非常严重的弊端:
1. Python中没有原生的二分法方法,第三方的类库还要结合 Pandas 来完成,期间需要做一些数据转换,这些都必然会带来一些不必要的开销。
2. Python的多线程是假多线程,实际上不支持多线程并行,这也是 Python 不能成为本任务工具的重要原因。
关系数据库的 SQL 也无法高效完成。这个聚类运算本质上是个非等值连接,数据库对于等值连接还能采用 HASH JOIN 等优化方案来减少计算量,但对于非等值连接就只能采用遍历方案了;SQL 也无法在语句中实现上面设计的复杂过程,不能识别距离的单调性而主动排序并采用二分法;再加上本来做这类数学类计算的能力不足(距离计算涉及三角函数);所以发生了前面实验阶段中 SQL 的单核性能还跑不过 Python 的现象。
Java等高级语言虽然可以实现二分法,也可以很好的并行,但代码写起来冗长,开发效率过低,会严重影响程序的可维护性。
那么,还能用什么工具来完成这个任务呢?
集算器 SPL 是个很好的选择,它内置了很多高性能算法(如二分法),也支持多线程并行,代码写起来也简单明了,还提供了友好的可视化调试机制,能有效提高开发效率,以及降低维护成本。
实际效果
相较于 Python 来说,SPL 为本任务提速 2000 倍,二分法能够提速 500 倍,多线程并行又提速 4 倍(笔者笔记本电脑的 CPU 只有 4 核),总计提速 2000 倍,使用 SPL 完成 500 多万目标规模的聚类任务只需要数个小时。
SPL的代码不仅性能优异,而且也并不复杂,关键计算代码只要 23 行。
A |
B |
C |
D |
E |
|
1 |
=RThd |
/距离阈值 |
|||
2 |
=NJob=4 |
/并行线程数 |
|||
3 |
=file("BasePhoto.csv").import@tc() |
||||
4 |
=directory@p(OtherPhotos) |
/其他照片路径 |
|||
5 |
for A4 |
=file(A4).import@tc() |
/其他照片 |
||
6 |
=B5.sort@m(OnOrbitDec) |
/排序 |
|||
7 |
=B6.min(DEC) |
||||
8 |
=delta_ra=F(B7,RThd) |
/根据DEC算RA阈值 |
|||
9 |
=FK(B5,NJob) |
/数据索引分段 |
|||
10 |
fork B9 |
=B5(B10) |
/照片片段 |
||
11 |
for A3 |
=C11.OnOrbitDec |
/DEC |
||
12 |
=D11-delta_rad |
/DEC下限 |
|||
13 |
=D11+delta_rad |
/DEC上限 |
|||
14 |
=C11.RA |
/RA |
|||
15 |
=D14-delta_ra |
/RA下限 |
|||
16 |
=D14+delta_ra |
/RA上限 |
|||
17 |
=C10.select@b(between@b(OnOrbitDec,D12:D13)) |
/二分查找DEC |
|||
18 |
=D17.select(RA>=D10&&RA<=D11) |
/查找RA |
|||
19 |
=D18.select(Dis(~,C11)<=A7) |
/细筛 |
|||
20 |
if D19!=[] |
/合并结果 |
|||
21 |
=FC(C11,D37) |
||||
22 |
=@|B10 |
/汇总结果 |
|||
23 |
=file(OFile).export@tc(B22) |
/写出结果 |
|||
B10格的 fork 是多线程并行函数,允许分段执行上述算法。
B6格的 sort@m() 函数是并行排序方法,数据量大时可以提高效率,数据有序是二分法使用的前提条件。
C17格的 select@b(...) 函数是二分查找方法,也是本任务提速的关键。
后记
性能优化的问题依赖于高性能的算法,只有把计算量降下来才能有效提高运行效率,而高性能算法需要在工作中慢慢积累,感兴趣的同学可以来这里学习常用的性能优化算法:性能优化课程。
高性能算法需要高效的编程工具来实现,之前已经说过,Python、SQL、java 等语言都有其弊端,要么无法并行,要么实现困难、维护困难。SPL 有足够的算法底层支持且允许高并发,代码能做到很简洁,还提供了友好的可视化调试机制,能有效提高开发效率,以及降低维护成本。



